Ultrakoude gassen (2): koud, kouder, koudst

Afbeelding 1. Een opstelling om atomen mee af te koelen.Foto: Florian Schreck.

In het eerste deel van deze serie introduceerden we de eerste fase die gebruikt wordt bij het afkoelen van een gas naar zeer lage temperaturen. De betreffende methode was die van laserkoeling, waarbij door het opnemen van een foton en het vervolgens spontaan uitzenden van een foton, een atoom zoals een strontiumatoom geleidelijk tot stilstand wordt gebracht. Deze fase van laser koelen resulteert in een bundel van atomen die vertraagd wordt van enkele honderden meters per seconde tot grofweg 10 meter per seconde, maar ook bij die snelheid hebben de atomen nog steeds een aanzienlijke temperatuur. De volgende stap in ons proces is dus wellicht makkelijk te raden, maar moeilijk om uit te voeren: verder tot stilstand brengen! Het opvangen en vasthouden van deze atomen zal in dit artikel ook uitvoerig worden behandeld. Wij weten immers wáár de atomen stil moeten staan, maar de atomen zelf niet. Dit moeten we dus op de een of andere manier ‘duidelijk zien te maken’ aan de atomen. Als we de atomen niet vasthouden in een zogeheten ‘trap’ (val), zal onze atoombundel als geheel blijven doorvliegen, en moeten we dus een heel groot laboratorium hebben. Op zich zou dit overigens geen probleem zijn: experimenten met koude gassen duren typisch slechts enkele secondes, en een laboratorium van enkele tientallen meters is zeker niet ondenkbaar. Het opvangen van de atomen in een trap heeft daarentegen nog andere voordelen: het stelt onderzoekers in staat om gemakkelijk het monster van atomen te bewerken met lasers om het nog verder af te koelen, en de uiteindelijke meting wordt ook iets eenvoudiger. Uiteraard is dit niet noodzakelijk: ons gas zou als geheel prima met een hoge snelheid naar rechts kunnen bewegen. Het einddoel, de temperatuur zo laag mogelijk krijgen, wordt daar niet door beïnvloed. Het gaat vooral om de onderlinge snelheden van de atomen die we willen elimineren.

Molasse-koeling

We gaan verder bij het punt waar we gebleven waren in het eerste deel van deze serie artikelen: een bundel atomen die met een relatief lage snelheid naar rechts beweegt. De bundel atomen beweegt echter niet alléén naar rechts. De atomen in de bundel kunnen ook een snelheidscomponent in een richting loodrecht op de gemiddelde beweegrichting hebben. Onze manier om atomen uit de oven te krijgen is immers niet perfect. Deze snelheden loodrecht op de bewegingsrichting leiden ertoe dat de bundel, als er niets tegen gedaan wordt, langzaam uitspreidt en een steeds grotere doorsnede krijgt. Aan het begin van ons afkoelproces was dit geen probleem. De ongewenste componenten van de snelheid die loodrecht stonden op de gewenste beweegrichting waren daar nog relatief erg klein. Aan het einde van de zeeman-slower is deze component echter wel significant. We moeten vanaf nu dus de atomen afremmen in álle richtingen, en niet alleen in de bewegingsrichting naar rechts. De methode die hiervoor gebruikt wordt kun je wellicht al raden: wederom laserkoeling. Maar nu laserkoeling vanuit alle richtingen in plaats van uit één enkele richting. Afbeelding 2 is een foto van onze ‘koelkast’ in het laboratorium, waarin de zeeman-slower en de bijbehorende atoom- en laserbundels aangegeven staan. Direct grenzend aan de zeeman slower gaan we beginnen met het afremmen van de atomen vanuit alle andere richtingen.

Afbeelding 2. Een setup voor het afkoelen van atomen zoals strontium.Aangegeven is waar de oorspronkelijke bundel vandaan komt, en waar de zeeman-slower en bijbehorende laserstraal zich bevinden. De Molasse-koeling en bijbehorende Magneto Optical Trap bevinden zich direct rechts van de zeeman-slower. Afbeelding: Florian Schreck (bewerkt).

In afbeelding 3 is een schematische weergave te zien van een opstelling waarin we van alle kanten de atomen afremmen. De manier waarop atomen hier worden afgeremd is precies hetzelfde als in de zeeman-slower: atomen bewegen tegen de richting van het laserveld, absorberen een foton, en zenden het vervolgens in een arbitraire richting uit, wat resulteert in een netto terugslag voor het atoom tegen zijn bewegingsrichting in. De naam van deze koelmethode, ‘Molasse-koeling’ wordt hiermee ook duidelijk: we maken het de atomen moeilijk om in welke richting dan ook te bewegen, precies zoals het zou zijn om jezelf voort te bewegen in molasse,een enorm stroperige substantie.

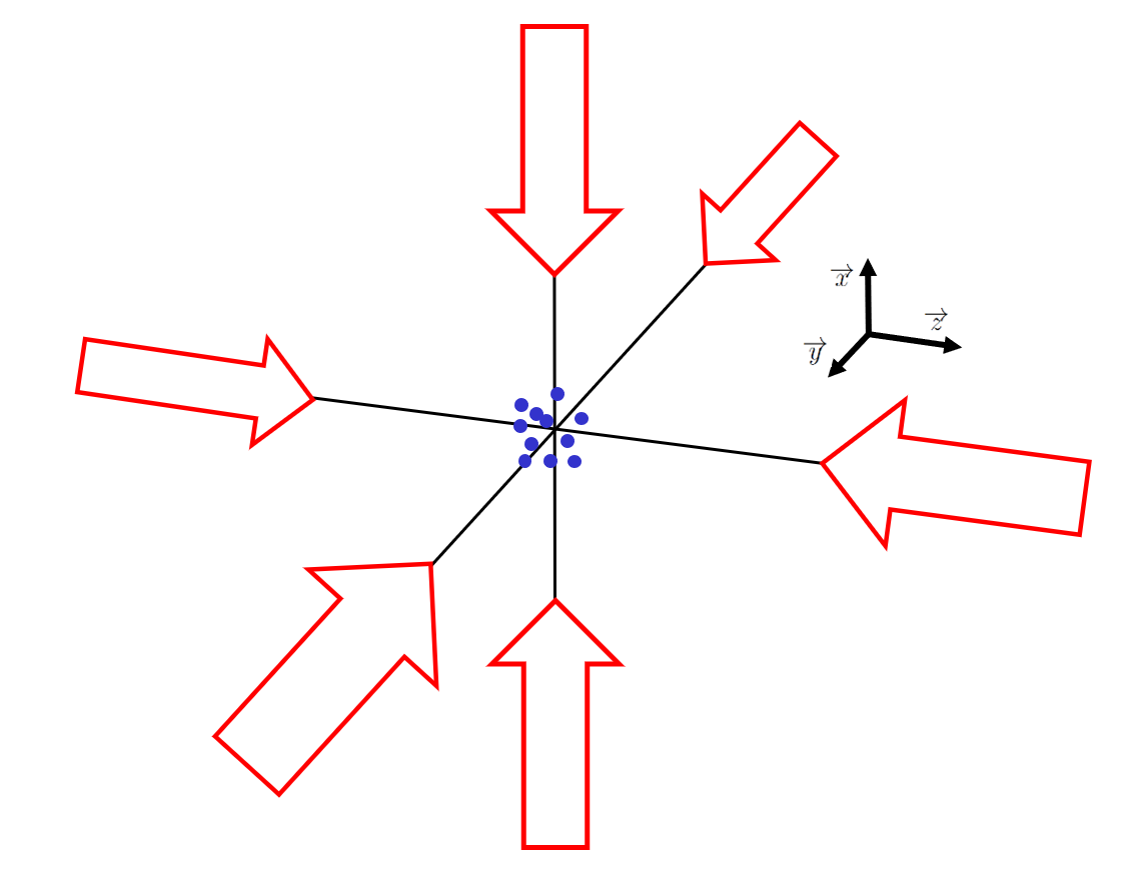
Afbeelding 3. Molasse-koeling.Atomen worden afgeremd door uit alle richtingen met lasers te koelen. Afbeelding: Florian Schreck.

De Magneto Optical Trap

Ik heb nu al veel verteld over hoe een straal atomen afgeremd wordt. Afremmen alléén is echter niet genoeg. Het kunnen beïnvloeden van de snelheid van onze atomen is nuttig, maar het is pas relevant als we ook aan onze atomen kunnen vertellen op welk punt ze stil moeten komen te staan. Dit kunnen we doen door ons systeem voor Molasse-koeling te upgraden naar wat een ‘Magneto Optical Trap’ heet. De naam verraadt al dat dit een methode is om atomen vast te houden door middel van een combinatie van magneetvelden en optische (laser-) velden. Ons doel is als volgt: als een atoom zich al bevindt op het punt waar het moet zijn, moeten we er niets meer mee doen. Als het ervandaan beweegt, moet het teruggeduwd worden. Het duwen van atomen wordt gedaan door onze lasers. We moeten dus ‘vertellen’ aan de atomen om fotonen pas op te nemen als ze op bepaalde plekken komen. Gelukkig kennen we al een mechanisme dat de energieovergangen (het absorberen van een foton is een voorbeeld van een energieovergang) van onze atomen kan beïnvloeden: Het zeemaneffect. Net zoals in de zeeman-slower, gebruiken we hier een magneetveld om de overgangsenergie van onze atomen te beïnvloeden, afhankelijk van de fysieke positie van het atoom. De plek waar onze atomen stil komen te staan noemen we ons punt ‘0’, de oorsprong. De sterkte van het magneetveld op dit punt maken we ook nul – oftewel: geen magnetisch veld op dit punt. Als een atoom wegbeweegt van de oorsprong, verlaagt het magneetveld, wat op die positie niet meer nul is, de energie die nodig is om onze atomen aan te slaan. We kunnen onze lasers hier precies op afstellen, zodat ze een energie hebben die overeenkomt met de rode pijlen zoals te zien onderaan afbeelding 4. Hierdoor wordt een foton alleen maar geabsorbeerd als het atoom zich niet op de juiste plek bevindt. Afbeelding 4 geeft een schematische weergave weer van wat hier beschreven is, in één richting (bijvoorbeeld langs de x-as).

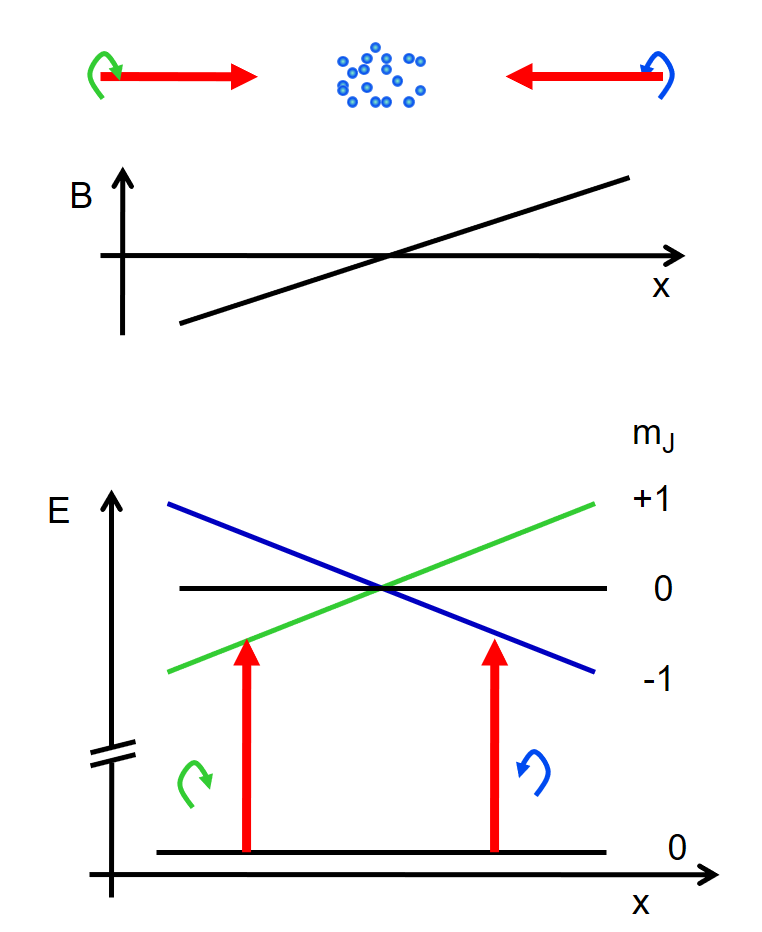
Afbeelding 4. Atomen naar de juiste plaats leiden.Grafieken die schematisch aangeven waar onze atomen zich moeten bevinden (de blauwe punten bovenaan), hoe de configuratie van het magneetveld (B) is (de tweede grafiek), en hoe de energieniveaus van het atoom aangepast worden aan de hand van dit magneetveld (onderste grafiek). De x-as van dit plaatje geeft de plaats van onze atomen weer. Op het punt waar het magneetveld nul is, definiëren we de oorsprong, x=0. De blauwe en groene lijn komen overeen met aangeslagen toestanden van het atoom met bepaalde impulsmomenten: groen is ‘met de klok mee draaiend’ en blauw is ‘tegen de klok in’. Afbeelding: Florian Schreck.

Met dit systeem zijn we er echter nog niet helemaal. Immers, onze laserstralen komen van alle kanten. In afbeelding 4 komen ze bijvoorbeeld uit zowel de negatieve x-richting als de positieve x-richting. Momenteel weten onze atomen alleen maar of ze zich wél of níét op de gewenste plaats bevinden. Nu moeten we de atomen nog vertellen aan welke kant van ons nulpunt ze zich bevinden. Hiervoor maken we gebruik van de heilige graal van de natuurkunde: behoud van impuls. Of liever, we maken gebruik van behoud van draai-impuls. De onderste 2 grafieken in afbeelding 4 vertellen ons wat er gebeurt met de energieniveaus van onze atomen afhankelijk van de positie van de atomen langs de x-as. De kleur van de lijnen geeft nog wat extra informatie: die vertelt ons iets over de draai-impuls die hoort bij die quantumtoestand (bedenk dat een energieniveau altijd hoort bij een bepaalde quantumtoestand van een atoom). Voor dit artikel is het voldoende om het volgende te weten over een atoomstructuur: elk atoom staat een elektron toe om zich in slechts bepaalde ‘toestanden’ (beschreven door golffuncties) te bevinden.

Elke toestand heeft bepaalde eigenschappen. De meest kenmerkende eigenschappen zijn energie, draai-impuls en spin. Zo kan een elektron in onze strontiumatomen bijvoorbeeld ‘met de klok meedraaien’ of ‘tegen de klok in draaien’. Laten we zeggen dat groen staat voor een draai-impuls met de klok mee, en blauw tegen de klok in. Als we een atoom vanuit de grondtoestand met de laagste energie willen brengen naar zijn aangeslagen toestand (en het daarmee een impuls-‘kick’ geven), moeten we, naast de energie die daarvoor nodig is, ook de benodigde draai-impuls meegeven. Alleen zo kunnen we voldoen aan de wetten voor behoud van energie én impuls. Als we onze laser straal au-naturel op onze atomen schieten, komt dit vanzelf goed. De laserstraal bevat in principe on-gepolariseerd licht, wat betekent dat het alle soorten van draai-impuls met zich meedraagt. Dit betekent dat we onze atomen zonder problemen kunnen aanslaan, omdat er altijd wel een foton is dat aan de gestelde eisen (de juiste energie en draai-impuls) voldoet.

We kunnen hier echter ook op selecteren! We kunnen er nu voor kiezen om alleen fotonen uit de negatieve x-richting te laten komen, die een draai-impuls met de klok mee hebben. Het zeeman-effect zorgt er namelijk niet alleen voor dat de benodigde energie minder wordt. Het zorgt er ook voor dat de energie van specifieke aangeslagen toestanden minder wordt: die toestanden met een bepaalde draai-impuls, zoals groen (met de klok mee), of blauw (tegen de klok in). Dit betekent dat een laserstraal die van links komt alleen maar aangeslagen toestanden naar de groene lijn kan waarmaken. Vanuit de positieve x-richting laten we nu alleen gepolariseerd licht toe dat een draai-impuls heeft tegen de klok in. Deze lichtstraal kan alleen naar het blauwe energie-niveau aanslaan.

Nu hebben we ons doel bereikt: een atoom dat zich links van de oorsprong bevindt, kan een foton opnemen, maar door behoud van draai-impuls, doet het dit alleen vanuit de laserstraal die van links komt. De laserstraal die van rechts komt heeft immers een ander impulsmoment (blauw) en kan alleen maar exciteren naar de blauwe lijn. Hiervoor heeft deze laser niet genoeg energie, waardoor deze laser links van de oorsprong geen effect heeft. Dit proces is rechts van de oorsprong precies andersom. Op deze manier kunnen we aan onze atomen ‘vertellen’ waar we ze stil willen laten staan: in de oorsprong.

Intermezzo: Polarisatie

Laat ik kort herhalen wat er bedoeld wordt met de ‘polarisatie’ van een (licht)golf. Sommige lezers zullen bekend zijn met de volgende twee termen: een transversale golf en een longitudinale golf. Een transversale golf is een golfbeweging die oscilleert loodrecht op de bewegingsrichting. Een longitudinale golf oscilleert juist parallel aan de bewegingsrichting. Polarisatie kun je je met name bij een transversale golf goed voorstellen. De oscillatie kan daar namelijk in twee verschillende richtingen plaatsvinden: trillend ‘omhoog en omlaag’, of trillend naar ‘links en rechts’. Dit heet lineaire polarisatie van een golf. Het kan echter ook zijn dat we te maken hebben met een combinatie van deze twee trillingen (links-rechts én op-en-neer), wat resulteert in zogeheten ‘circulaire’ polarisatie. Licht (elektromagnetische golven), maar ook andere golven, hebben door deze circulaire polarisatie een draai-impuls. De golven roteren bij circulaire polarisatie als het ware rondom de bewegingsrichting. De draai-impuls van licht is wel zeer klein – zo klein, dat het zelfs vandaag de dag nog moeilijk te meten is. Desondanks is het er, en we zien het effect hiervan terug in onder andere onze Magneto Optical Trap.

Afbeelding 5. Een voorbeeld van polarisatie.Het rubberen touwtje heeft rechts in de afbeelding een circulaire polarisatie. Door de gleuf tussen de twee metalen staven wordt één polarisatiecomponent ‘uitgefilterd’, waardoor er lineaire polarisatie overblijft. Copyright: https://creativecommons.org/licenses/by-sa/3.0/, bron: https://en.wikipedia.org/wiki/Polarization_(waves)#/media/File:Polarizacio.jpg (Wikipedia).

De technieken die we nu hebben besproken, stellen ons in staat om een gas flink af te koelen. We lopen daarbij wel tegen een grens aan: de Dopplerlimiet. We kunnen een gas van atomen namelijk niet oneindig ver afkoelen door het ‘af te remmen’. Als een atoom een foton opneemt en weer uitzendt, krijgt het door de terugslag een ‘trap’ in een bepaalde richting. Je kunt je misschien wel voor stellen dat we op een gegeven moment een evenwicht bereiken, waarbij de impulsoverdracht van de lasers op de atomen die deeltjes evenveel ‘opwarmen’ (in beweging brengen) als ‘afkoelen’ (tot stilstand brengen). Deze grens heet de Dopplerlimiet. De temperatuur die in de limiet bereikt kan worden, verschilt per type atoom waaruit een gas bestaat, maar bedraagt meestal enkele honderden microkelvin. Deze temperatuur is helaas nog te hoog voor onze doeleinden. We moeten proberen om af te koelen tot enkele honderden nanokelvins, enkele ordes van groter lager, om interessante natuurkunde tegen te komen zoals de vorming van een Bose-Einsteincondensaat, of een supervloeistof.

Een gelukkig ongeluk

Vaak gaan dingen niet zoals gepland. Toen de Magneto Optical Trap (MOT in het kort) bedacht werd, en vervolgens getest, hoopten de ontwerpers natuurlijk dat die werkte zoals voorspeld. Dit deed het apparaat niet… het werkte beter.

Afbeelding 6 is een grafiek uit het artikel ‘Observatie van atomen die gekoeld zijn tot onder de Dopplerlimiet’, gepubliceerd op 11 juli 1988.

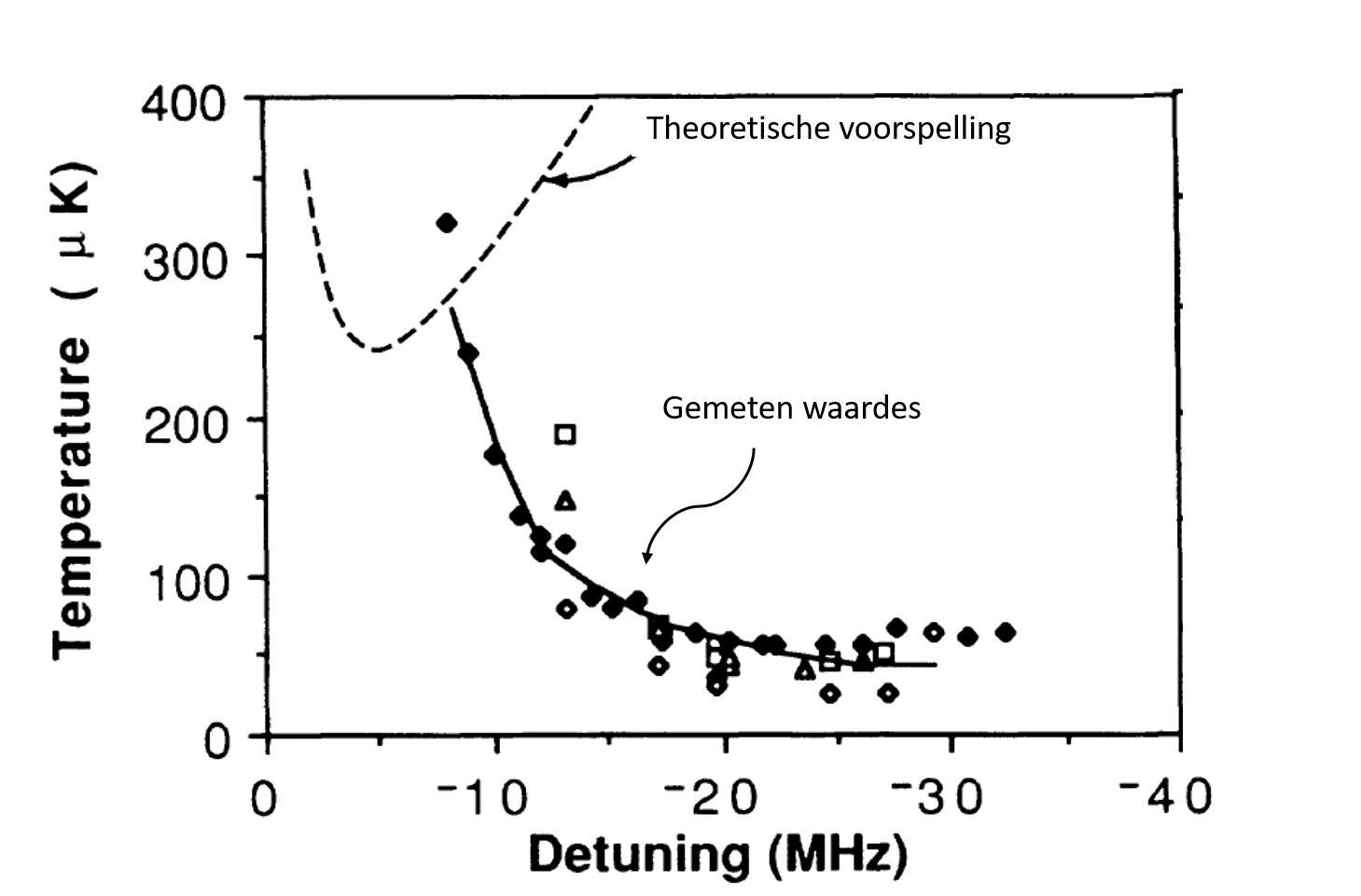
Afbeelding 6. De grafiek uit het artikel van 1988.Op de verticale as staat de temperatuur uitgezet, en op de horizontale as de ‘detuning’. Dit is de mate waarin de energie van de laser verschilt van de precieze energieovergang van het atoom. De theoretische voorspelling is de gestreepte lijn bovenin. De gemeten waardes zijn de punten onderin de grafiek, bij temperaturen die driemaal zo laag waren als voorspeld. Bron: Physical Review Letters.

De auteurs rapporteerden dat hun monster van natrium enkele malen kouder werd dan het theoretische model voorspelde. Dit stelde de auteurs voor een raadsel. Waarom werkte hun ‘koelkast’ zoveel beter dan gedacht? Een jaar later bedacht de Franse natuurkundige Claude Cohen-Tannoudji een theoretische verklaring voor dit fenomeen. De naam die tegenwoordig gegeven wordt aan zijn verklaring is ‘Sisyphuskoeling’, naar de Grieks-mythologische figuur Sisyphus. Deze verklaring en vele andere ontdekkingen hebben er uiteindelijk toe geleid dat Tannoudji in 1997 de Nobelprijs voor de Natuurkunde mocht ontvangen voor de ontwikkeling van methodes om atomen af te koelen en vast te houden met behulp van lasers.

Sisyphuskoeling

Je vraagt je wellicht af waar de naam ‘Sisyphuskoeling’ vandaan komt. De naam is afkomstig van de mythologische koning Sisyphus, die door de goden veroordeeld was om continu een zware bal een steile helling op te duwen. Sisyphuskoeling baseert zich op een vergelijkbaar fenomeen, waarbij een atoom het gevoel heeft dat het, als het een bepaalde richting op beweegt, ook altijd tegen een helling op moet. Hierdoor zal het steeds langzamer gaan bewegen en dus afkoelen. Het mechanisme berust wederom op de polarisatie van licht. Zoals hiervoor al gezegd, gebruiken we bij een MOT laserstralen die van verschillende, tegenovergestelde kanten komen. Dit betekent dat we op elk punt in de ruimte licht van de ‘linker’ lichtstraal hebben, en licht van de ‘rechter’ lichtstraal. Dit betekent weer dat we op elk punt in de ruimte eigenlijk moeten kijken naar de som van de twee lichtstralen. Beide lichtstralen bestaan voor de helft uit een oscillerend elektrisch veld met een circulaire polarisatie; de andere helft is een oscillerend magnetisch veld. Omdat we naar de som van de twee lichtgolven kijken, kan het zijn dat de polarisaties van deze elektrische velden op sommige plekken in de MOT elkaar versterken, wat leidt tot een bepaalde ‘totale’ polarisatie, en op andere plekken juist elkaar uitdoven. In afbeelding 7 heten deze twee fases σ^– en σ⁺. Het elektrisch veld met de polarisatie σ^± heeft een bepaalde wisselwerking met onze atomen, waardoor sommige quantumtoestanden van het atoom weer een lagere energie krijgen dan andere. Als het elektrische veld van de laser er niet was, zou dit niet gebeuren. Dit effect is zéér klein, maar als het maar lang genoeg aanhoudt, zal het een zeer meetbaar effect hebben op onze atomen.

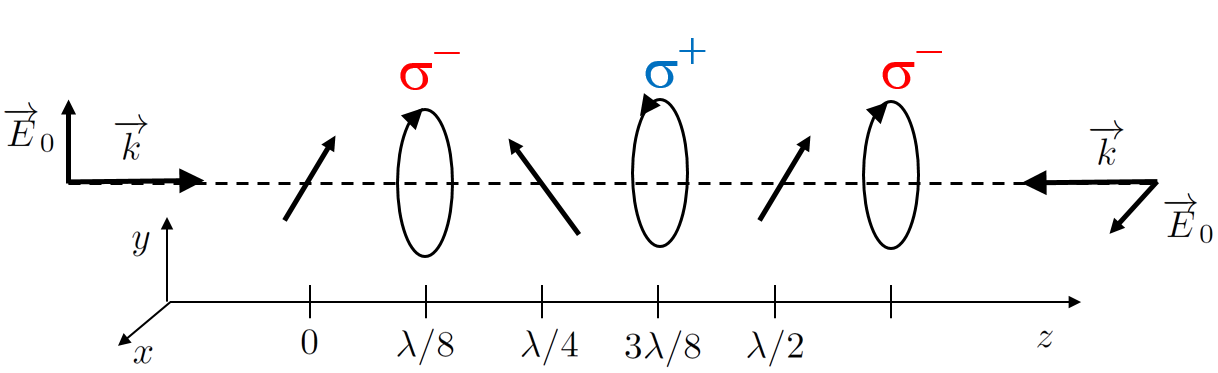
Afbeelding 7. Polarisatie optellen.Elektrische velden (E₀) waaruit het laserlicht bestaat, schijnen van links en rechts langs (bijvoorbeeld) de z-as. Beide elektrische velden hebben een polarisatie die kan optellen tot een lineaire polarisatie, of een circulaire polarisatie linksom (σ⁺) of rechtsom (σ^–). Wáár dit gebeurt, hangt af van de fysieke coördinaten (x,y,z).

De polarisatie van het licht heeft natuurlijk nog steeds als gevolg dat sommige overgangen van energieniveaus niet (of juist wel) zijn toegestaan. Dit was immers de bedoeling in de MOT. In afbeelding 8 is een grafiek weergegeven waarin dit effect wordt samengevat. De blauwe en rode lijnen geven de energie van een bepaalde toestand weer. Zoals te zien is, is op sommige punten in de ruimte de energie van de blauwe toestand lager, en op andere punten die van de rode toestand.

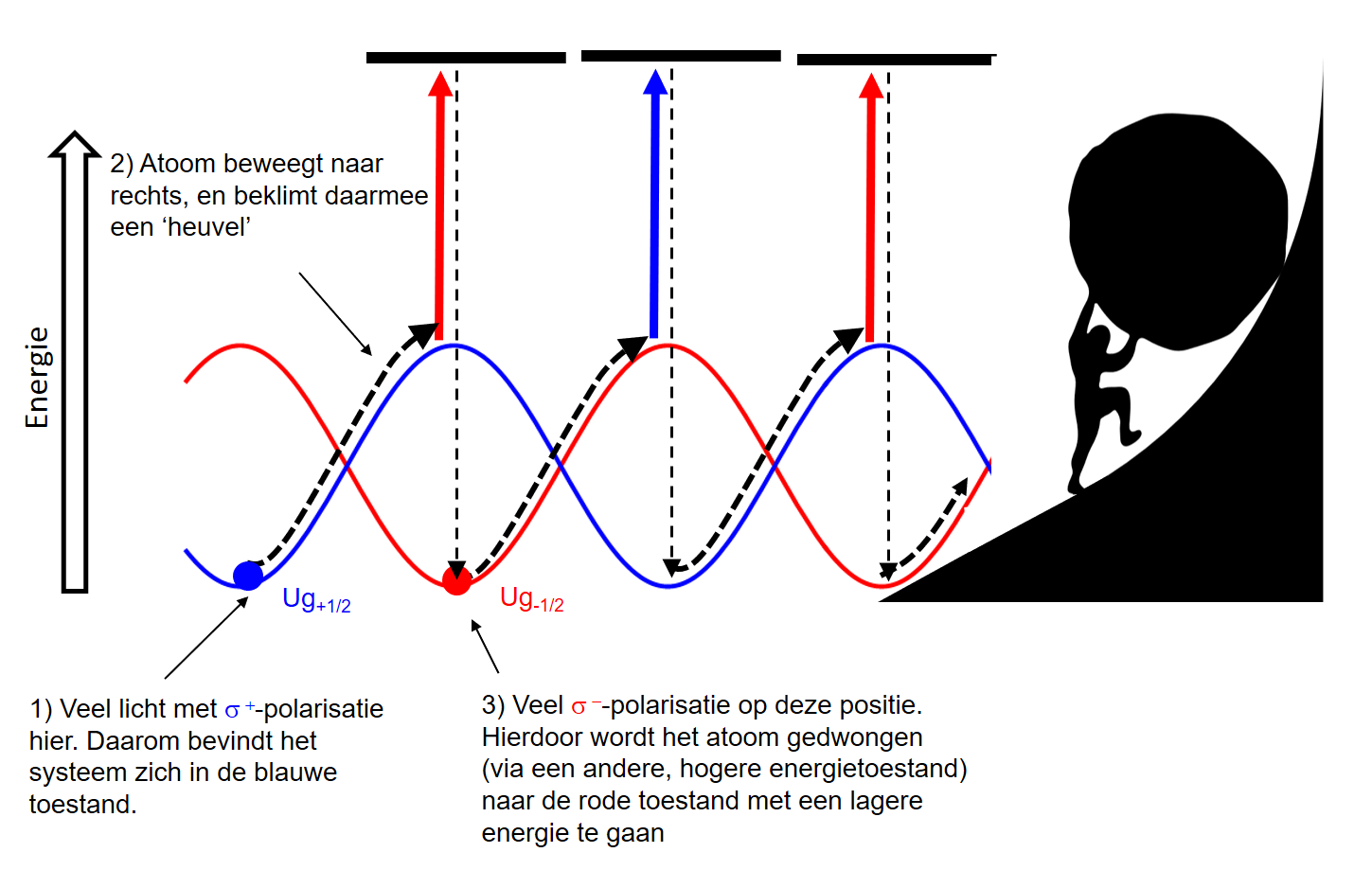
Afbeelding 8. Sisyphuskoeling.Een schematische weergave van Sisyphuskoeling. De hoogte in de figuur bepaalt de energie van de toestand. Bij stap 1 begint een elektron in de blauwe energietoestand; de polarisatie van het elektrisch veld duwt het atoom namelijk in die toestand. Vervolgens heeft het atoom een snelheidscomponent naar rechts. De polarisatie van het E-veld verandert afhankelijk van de plaats, en de energie die hoort bij de blauwe toestand wordt hoger. De energie hiervoor moet gehaald worden uit kinetische energie (stap 2). Vervolgens komt het atoom op een punt waar het via een hoge-energietoestand (door standaard laserkoeling) gedwongen wordt naar de rode toestand (stap 3) ). Afbeelding: Florian Schreck (bewerkt) en Public Domain Vectors.

Stel je een atoom voor dat zich links in de afbeelding bevindt. Het atoom zit in een bepaalde voorkeurstoestand met laagste energie (bijvoorbeeld in het dal van de blauwe lijn). Doordat het atoom nu naar rechts beweegt, wordt de samenstelling van het elektrisch veld van het licht anders (door de twee lasers die tegenover elkaar staan) en wordt de energie die hoort bij de toestand van de blauwe lijn verhoogd. Dit betekent dat er energie in het atoom moet worden gestopt. Deze energie moet ergens vandaan komen, en de enige beschikbare bron is de kinetische energie van het atoom, precies die energie die we wilden onttrekken aan het atoom om het tot stilstand te krijgen. Op een gegeven moment komt ons atoom bij de ‘top’ van de blauwe lijn aan. Op dit punt in de ruimte is de configuratie van ons licht heel anders. De polarisatie van het licht dwingt ons atoom om naar de toestand te gaan die overeenkomt met de rode lijn. Deze toestand heeft een lagere energie dan de toestand van het atoom op de blauwe lijn. Om van de blauwe toestand naar de rode toestand te komen, moet het atoom fotonen absorberen en vervolgens weer uitzenden. Op die manier raakt het energie kwijt aan de omgeving. Als het atoom nu verder beweegt, moet het weer een heuvel beklimmen, en zal het weer terugvallen naar een lagere-energietoestand, daarbij weer een klein beetje kinetische energie verliezend. Dit constant ‘heuvelopwaarts’ bewegen van het atoom is de reden dat dit mechanisme Sisyphuskoeling heet, en het is er de oorzaak van dat de Magneto Optical Trap zo veel efficiënter werkt dan oorspronkelijk werd gedacht.

Als dit proces doorlopen wordt met bijvoorbeeld strontiumatomen, komen die uit bij een temperatuur van ongeveer 1 microkelvin. Rubidium kan tot ongeveer 30 microkelvin worden gekoeld. De verschillen tussen de twee soorten atomen komen vooral door verschillen in de atoomstructuur tussen de twee elementen. De bereikte temperatuur lijkt al fantastisch klein, maar is nog stééds niet genoeg om ons doel te halen: Een Bose-Einsteincondensaat. Hiervoor moet nog gebruikt gemaakt worden van een laatste techniek: evaporative cooling. Met deze koeling kunnen we ons gas afkoelen tot de temperatuur die we echt willen bereiken: enkele honderden nanokelvin. Daarbij is, zoals hierboven beschreven, onze methode om het gas vast te houden niet meer geschikt. Die methode bereikt de Dopplerlimiet, waar de terugslag van het absorberen van fotonen een even groot verwarmend als afkoelend effect heeft. Niet alleen moeten we verder koelen, we zullen dus óók een nieuwe methode moeten vinden om ons gas vast te houden. Deze laatste twee methodes zullen worden beschreven in het volgende en laatste artikel in deze serie over het maken van een ultrakoud gas.