In de afgelopen eeuw zijn er veel belangrijke en baanbrekende ontdekkingen in de natuurkunde gedaan. Zo bedacht Einstein zijn fascinerende theorie over zwaartekracht in 1915 en is het standaard model geformuleerd door middel van ideeën uit de kwantumveldentheorie. Achter de ontwikkeling van deze theorie zit een zeer fundamenteel concept in de natuurkunde: symmetrie.
Wat zijn symmetrieën nu precies?
Laten we beginnen met een eenvoudig voorbeeld om uit te leggen wat symmetrie precies is, zie ook het artikel symmetrieën in de natuurkunde voor meer detail. Stel we beschouwen een gelijkzijdige driehoek. Als we deze driehoek over een hoek van 120 graden om zijn zwaartepunt draaien, dan krijgen we precies dezelfde driehoek terug. Dit geldt ook voor een rotatie van 240 graden. We zeggen dan dat de rotaties over 120 en 240 graden symmetrieën van de driehoek zijn. Het zijn echter niet de enige symmetrieën van een gelijkzijdige driehoek. Als we bijvoorbeeld de driehoek spiegelen in een zwaartelijn zal de driehoek ook onveranderd blijven. De gelijkzijdige driehoek heeft drie van zulke zwaartelijnen en dus samen met de rotaties zijn er in totaal zes symmetrieën (waarbij we ‘niets doen’ ook hebben meegeteld). Een symmetrie is dus een operatie of transformatie van een object die het object onveranderd laat.
De symmetrieën van een gelijkzijdige driehoek zijn een voorbeeld van discrete symmetrieën. De rotaties zijn namelijk bepaalde vaste (discrete) hoeken en kunnen niet elke mogelijke waarde aannemen. Wanneer rotaties of andere transformaties van een object wel alle mogelijke waarden aan kan nemen, spreken we over een continue symmetrie. De cirkel heeft bijvoorbeeld een continue rotatie symmetrie. Welke rotatie we ook rondom het middelpunt uitvoeren, de cirkel blijft hetzelfde.
Relativistische natuurkunde en het theorema van Noether
Continue en discrete symmetrieën komen veelvuldig voor in de natuur. Neem bijvoorbeeld de kristalstructuur van keukenzout. Deze heeft dezelfde symmetrieën als een kubus en dus zijn er allerlei transformaties zoals rotaties over vaste hoeken en spiegelingen die de kristalstructuur onveranderd laten. Een voorbeeld van een veelvoorkomende continue symmetrie is die van de relativistische natuurkunde. Dit zijn erg belangrijke symmetrieën in de natuurkunde en werden ontdekt door de Nederlandse natuurkundige Hendrik Lorentz. Ze worden ook wel Lorentz transformaties genoemd en waren tevens de basis voor de speciale relativiteitstheorie van Einstein. Enkele andere belangrijke continue symmetrieën zijn translatie symmetrieën, die een punt x in de ruimtetijd naar een punt x + a sturen, voor een willekeurige vector a. Dit is een symmetrie, want in de lege ruimtetijd kun je geen onderscheid maken tussen verschillende punten in de ruimtetijd. De translatie symmetrieën vormen samen met de Lorentz transformaties, de Poincaré groep (een groep is een object in de wiskunde, waarvan de precieze betekenis nu niet van belang is).

Afbeelding 1. Albert Einstein (Links) en Hendrik Lorentz (Rechts)
Een foto van Lorentz en Einstein gemaakt door Paul Ehrenfest voor zijn huis in Leiden in 1921. Bron: Museum Boerhaave, Leiden.
In de relativistische natuurkunde is de Poincaré groep van groot belang. Elk relativistisch systeem is namelijk invariant onder de symmetrieën die in de Poincare groep zitten. Een relativistisch systeem heeft de bekende symmetrieën, zoals tijd- en ruimtetranslaties en rotaties, maar is ook invariant onder boostsymmetrieën. Deze laatste symmetrieën geven bijvoorbeeld aanleiding tot de bekende Lorentzcontracties in tijd en ruimte. Daarnaast is er nog een veel ingrijpender gevolg van het hebben van een symmetrie.
De Duitse wiskundige Emmy Noether liet namelijk zien dat als een bepaald systeem een symmetrie bevat er een bijbehorende behouden grootheid is. Dit betekent dat een symmetrie een waarneembaar effect heeft en ervoor zorgt dat bepaalde grootheden niet in tijd veranderen. Het eenvoudigste voorbeeld van Noether’s theorema is behoud van energie. Als een systeem een tijdstranslatie symmetrie bevat, dan heeft het een behouden grootheid, namelijk de energie. Dezelfde relatie geldt tussen ruimtelijke translaties en behoud van impuls, en rotatiesymmetrieën en behoud van hoekimpuls. Symmetrieën van een systeem hebben dus verregaande gevolgen, niet alleen maar voor waarneembare effecten, maar ook vanuit puur theoretische oogpunt.
Theorieën bouwen met symmetrie
Voor de theoretische fysicus is symmetrie namelijk een goede vriend. Het vertelt hen welke theorieën wat voor behouden grootheden hebben en helpt hen ook bij het ‘bouwen’ van een theorie. Het is vaak voorgekomen in de natuur dat er metingen gedaan werden die lastig te verklaren waren, maar waarbij men wel wist welke symmetrieën er aanwezig waren. Theoretische fysici nemen de symmetrieën dan als startpunt om een theorie op te schrijven die de metingen bij benadering kan verklaren. Het kan bijvoorbeeld zo zijn dat deze ‘trial’ theorie niet de meting precies kan verklaren, maar qua order van grootte hetzelfde is. Het geeft dan geen inzicht in de precieze natuurkunde achter de meting, maar geeft een schatting voor welk fysisch mechanisme de grootste bijdrage levert. Vaak werken deze theorieën erg goed bij bepaalde energieën, maar slecht bij andere energieën. Een mooi voorbeeld hiervan is zwaartekracht. De theorie van Einstein werkt erg goed bij grote afstanden, maar op heel kleine afstanden is het duidelijk geworden dat deze theorie niet meer goed werkt. Er zijn nieuwe effecten van de fysica van zwarte gaten die we niet kunnen verklaren met de theorie van Einstein. Om deze effecten wel te kunnen verklaren zijn theoretische fysici al een aantal decennia bezig om een nieuwe theorie van zwaartekracht te ontwikkelen, wederom met symmetrie als basis principe.
Weg met die symmetrie!
De aanwezigheid van een symmetrie betekent dus volgens Noether dat er een behouden grootheid is, maar wat gebeurt er als die symmetrie gebroken wordt en niet meer aanwezig is? Noethers theorema geldt dan niet meer en de grootheid die met symmetrie nog behouden was is dat nu simpelweg niet meer. Toch kunnen theoretisch fysici door de manier van breking erg veel te weten komen over de achterliggende natuurkunde en vormt vaak een belangrijk mechanisme om bepaalde metingen te kunnen verklaren.
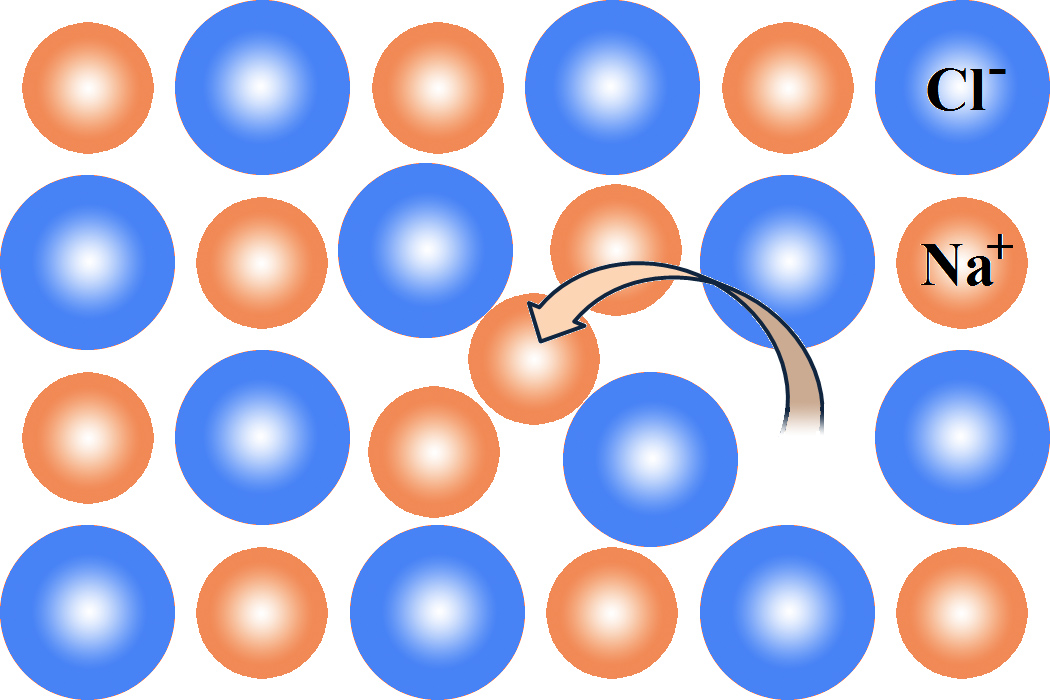
Afbeelding 2. Symmetriebreking
Een natrium atoom in keukenzout (NaCl) verspringt van plaats en breek zo de symmetrie van het kristal. Dit effect wordt ook wel het Frenkel effect genoemd. Bron: wikipedia-gebruiker VladVD.
Het breken van een symmetrie kan op verschillende manieren gebeuren. Grofweg kunnen die manieren in twee groepen verdeelt worden, expliciete breking en spontane breking. Als een symmetrie expliciet gebroken wordt is het geen symmetrie meer van de theorie. Dit gebeurt bijvoorbeeld doordat een elektrisch veld in de z-richting rotatiesymmetrieën om de x- en y-as breekt. Spontane symmetriebreking is wat subtieler en betekent niet dat de theorie de symmetrie niet meer heeft, maar dat alleen bepaalde toestanden, zoals het vacuum, de symmetrie breken. Deze vorm van symmetriebreking komt veelvuldig voor in de natuur en vormt de verklaring voor supergeleiding en het Higgs-deeltje!
Symmetrieën kunnen ons veel vertellen over welke fenomenen we in de natuur waarnemen. De relatie tussen behoudswetten en symmetrie vormt daarbij een cruciale rol en speelt nog steeds een belangrijke rol in het ontwikkelen van nieuwe theorieën. Zonder het concept symmetrie zouden we nooit zo ver in ons begrip van de natuur zijn gekomen. Het zal dan ook zeker nog een leidende rol hebben in alle natuurkundige waarnemingen die we tot nu toe nog niet begrepen hebben.
_______________________________________________________________________
Dit arikel verschijnt ook in De Physicus, tijdschrift van de Vereniging voor Technische Physica Delft.