
Afbeelding 1. Sterke koppeling.Als de onderdelen van een systeem sterk met elkaar wisselwerken – als er een grote kracht werkt, dus – spreken we in de natuurkunde van ‘sterke koppeling’. Afbeelding: Daniel Schwen.
In de natuur zijn er veel fenomenen die we met zwak of zelfs niet wisselwerkende deeltjes kunnen beschrijven. Een voorbeeld is de interactie tussen licht en materie: de twee reageren wel op elkaar, maar de interactie is niet heel sterk. Dat is voor natuurkundigen een hele opluchting, want met zo’n ‘zwak gekoppelde’ beschrijving kunnen we veel dingen uitrekenen, en mooie voorspellingen doen door middel van storingsrekening.
Dat alles had natuurlijk niet per sé zo hoeven zijn, en andere interacties in de natuurkunde zijn veel sterker. Wat doen we als er geen mogelijkheid is om een verschijnsel met zwak gekoppelde deeltjes te beschrijven? Kort gezegd: niet zo veel – het blijft tot op de dag van vandaag een uitdaging om iets zinnigs te zeggen over zulke theorieën. Toch is er in de afgelopen decennia een aantal mooie en slimme technieken ontwikkeld, waarmee we ook het een en ander kunnen zeggen over een sterk gekoppelde theorie. Wat die technieken precies zijn en waar in de natuur deze sterk gekoppelde theorieën voorkomen, zal ik in dit artikel bespreken.
Het Kondomodel
Een van de plekken waar sterk gekoppelde fysica zijn intrede doet, is in een metaal met een handjevol magnetische onzuiverheden: andere atomen in het metaal die een netto magnetisch moment hebben. Het model dat dit systeem beschrijft wordt ook wel het Kondomodel genoemd, naar de natuurkundige Jun Kondo.
Bij hoge temperaturen hebben de onzuiverheden geen effect op de geleidingseigenschappen van het metaal en is de theorie die het metaal plus onzuiverheden beschrijft zwak gekoppeld. Gaan we nu naar heel lage temperaturen, ongeveer 1 Kelvin, dan verandert dit beeld. De theorie die dit systeem van het metaal en onzuiverheden beschrijft is nu niet meer zwak gekoppeld, maar juist sterk gekoppeld. Bij lage temperaturen gaan de elektronen zich namelijk binden aan de magnetische onzuiverheden, en zo gebonden toestanden vormen. Als gevolg hiervan daalt de elektrische geleiding een beetje en gedraagt het metaal met onzuiverheden zich bij lage temperaturen meer als een isolator dan als een zuiver metaal.
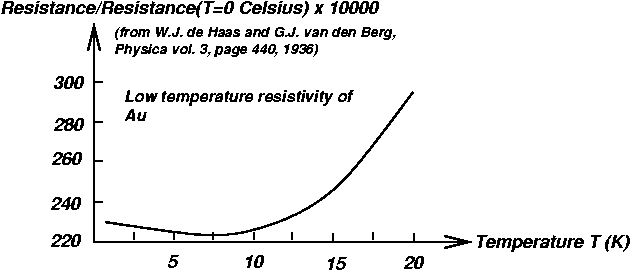
Afbeelding 2. Meting weerstand van goud bij lage temperaturen.Een meting van De Haas en Van de Berg in 1936 van de weerstand van goud bij lage temperaturen. Door de aanwezige magnetische onzuiverheden in het metaal gaat de weerstand iets omhoog in plaats van omlaag bij heel lage temperaturen. Dit effect noemen we het Kondo-effect. Afbeelding: Wikipediagebruiker Bkell.
De sterke koppeling bij lage temperaturen komt door het feit dat de koppelingsconstante – de maat voor de sterkte van de interactie – in deze theorie niet echt een constante is, maar van temperatuur afhangt. (Zie ook het artikel over renormalisatie.) Het blijkt dat deze koppelingsconstante heel klein is bij hoge temperaturen. We zeggen in zo’n geval dat de theorie asymptotisch vrij is. Bij een bepaalde lage temperatuur daarentegen blaast de koppelingsconstante juist op en kunnen we geen storingsrekening meer gebruiken om berekeningen te doen. Het is precies deze lage temperatuur, ook wel de Kondo-temperatuur genoemd, waar de gebonden toestanden beginnen te vormen.
Op het moment dat deze gebonden toestanden ontstaan, heffen de meeste natuurkundigen hun handen ten hemel en is er niet een heel goede manier om verdere voorspellingen doen. Het probleem is mede dat de fundamentele vrijheidsgraden bij hoge temperaturen – de elektronen en onzuiverheden – bij lage temperaturen niet meer de belangrijkste ‘bouwstenen’ van het model zijn. Ze worden ingeruild voor andere vrijheidsgraden: collectieve bewegingen van grote groepen deeltjes. Voor deze nieuwe vrijheidsgraden is het lastig om een theorie op te schrijven waar we dan weer storingstheorie op kunnen toepassen.
Quantumchromodynamica
Een ander voorbeeld van een theorie die bij lage energieën sterk gekoppeld is, is quantumchromodynamica (of ‘QCD’), de theorie van de sterke kernkracht. Deze theorie beschrijft quarks en hun krachtdeeltjes, gluonen, en bij lage energieen ontstaan er wederom gebonden toestanden van deze deeltjes. Deze toestanden vormen de bouwstenen van alles om ons heen: de baryonen en mesonen, waarvan het proton en het neutron de bekendste zijn – zie afbeelding 2. De gebonden toestanden zijn overigens beter te beschrijven als een soort soep van quarks en gluonen, dan als een vaste verzameling deeltjes die sterk aan elkaar gebonden zijn, doordat de koppeling zo groot is dat er telkens nieuwe deeltjes uit het vacuum gemaakt en vernietigd worden.
Afbeelding 3. Gebonden toestanden in QCD.In deze afbeelding zie je de soorten gebonden toestanden in de quantumchromodynamica. Drie gebonden quarks vormen een baryon, en een quark-antiquarktoestand noemen we een meson. De zwarte pijltjes tussen de quarks geven de gluonen weer. Deze interacties zijn wetenschappers sinds de jaren 60 gaan interpreteren als snaren. De kleuren geven de verschillende soorten kleurladingen in QCD aan. Afbeelding: Wikipediagebruiker Maschen.
Net zoals bij het Kondomodel is er in dit sterk gekoppelde regime weinig concreets te zeggen over de precieze natuurkunde die er gaande is. Anders gezegd: de theorie verliest zijn voorspelbaarheid bij lage temperaturen als we storingstheorie blijven gebruiken. Toch zijn wetenschappers er in de jaren 60 in geslaagd om een voorstel te formuleren om de nieuwe vrijheidsgraden bij lage energieën te beschrijven. Deze theorie zijn we al veelvuldig in soms heel andere gedaantes tegengekomen op deze site: het is de snaartheorie.
Snaartheorie
Om te begrijpen waarom wetenschappers met snaartheorie op de proppen kwamen, doen we het volgende gedachte-experiment. Stel: we nemen twee quarks, bijvoorbeeld gecombineerd in een meson (een quark en antiquark, zie afbeelding 2) en we trekken die langzaam uit elkaar. Bij hoge energieën (oftewel: op kleine afstandsschaal) gaat dit gemakkelijk, want dan is de theorie vrij en wisselwerken de quarks nauwelijks. Naarmate de afstand tussen de quarks groter wordt, wordt het steeds moeilijker om ze uit elkaar te trekken en worden ze sterk bij elkaar gehouden door de dragers van de sterke kernkracht: gluonen. Hoe meer we de twee quarks dan uit elkaar halen, hoe meer gluonen er ontstaan. Het inzicht dat de theoretici, voortbouwend op werk uit de jaren 60 hadden, is dat die gluonen tussen de quarks voorgesteld kunnen worden als snaren, kleine ’touwtjes’ die de quarks verbinden, en dat een beschrijving van QCD bij lage energieen dus wel eens iets met snaren te maken zou kunnen hebben.
Sinds dit idee ontstond, is er veel werk verricht aan het begrijpen van QCD met behulp van snaren. In de loop der jaren snaartheorie is men snaartheorie echter ook als iets veel fundamentelers gaan zien – een beschrijving van de zwaartekracht in plaats van (alleen) de sterke kernkracht. Al met al is er wel vooruitgang geboekt, maar is het nog steeds niet helemaal duidelijk hoe een snaartheoretische beschrijving van QCD er precies uitziet.
Hoe dan verder?
Snaartheorie bleek een manier om voortgang te boeken in het begrijpen van sterk gekoppelde theorieen, maar zo’n beschrijving is niet voor alle theorieën weggelegd. Het blijft lastig om kwantitatieve en algemeen geldende uitspraken te doen over sterk gekoppelde theorieën en er is nog veel onderzoek nodig om precies te begrijpen wat er in dit soort modellen gaande is.
Er zijn verschillende technieken ontwikkeld, zoals het bootstrapprogramma en het gebruik van dualiteiten zoals AdS/CFT, die een goede stap maken in die richting en voorspellingen kunnen doen over wat de nieuwe vrijheidsgraden zijn in het sterk gekoppelde regime van de theorie. Een andere manier is om storingstheorie te blijven gebruiken, maar heel goed te begrijpen hoe alle correcties eruit zien en ze wellicht allemaal op te sommen. Dit principe wordt ook wel resurgence genoemd en is al eens uitgebreid aanbod gekomen in een serie van drie artikelen (delen 5, 6 en 7 van het dossier over storingsrekening).
Sterk gekoppelde theorieën vormen dus voor veel theoretisch natuurkundigen nog een groot raadsel. Er zijn allerlei mysterieuze fenomenen gaande die we nog niet goed begrijpen en die nog jaren onderzoek vereisen om volledig te doorgronden. Hoe we dat zullen doen weten we natuurlijk niet, maar het is zeker dat dit onderzoek heel interessante technieken en begrip van de natuurkunde met zich mee zal brengen. Stay tuned!
In de zomerperiode verschijnen de Quantum Universe-artikelen éénmaal per week, op vrijdag. Vanaf september is de redactie weer terug van alle conferenties en vakanties, en verschijnen de artikelen weer tweemaal per week, op dinsdag en vrijdag.