
Afbeelding 1. Quasideeltjes.Een elektron-quasideeltje in een ionenrooster. Afbeelding: Martin W. Zwierlein, MIT.
Bewegen door een menigte
Stel je voor dat je zelf een elektron bent, dus een van de elementaire deeltjes in het standaardmodel. Je bent een fermion, dus je kunt je niet in precies dezelfde toestand bevinden als een ander elektron, en je hebt natuurlijk een massa (me), negatieve lading (e), spin (½), enzovoort. Normaal gesproken wordt de toestand waarin je verkeert beschreven door je golffunctie, en met behulp van de Schrödingervergelijking kunnen we uitrekenen hoe je je gedraagt. Hoewel… dat laatste klinkt redelijk, maar dat uitrekenen kunnen we in de praktijk alleen doen wanneer je je bevindt in een eenvoudige ruimte, zoals een lege kamer. De vorm van de kamer waar je in staat – waar de muren staan en of de vloer vlak is of niet – kunnen we zelfs meenemen in onze berekening.
Maar wat gebeurt er wanneer je niet door een lege ruimte beweegt, maar door een kamer gevuld met ‘andere mensen’ – andere deeltjes, dus? Dit maakt het probleem veel ingewikkelder, omdat net als in een echte mensenmenigte die mensen ook met je meebewegen, of je in de weg zitten, maar in ieder geval geen statische achtergrond meer vormen. Anders gezegd: we kunnen door alle wisselwerkingen tussen jouzelf en de mensen om je heen nu eigenlijk niet meer zeggen dat jouw toestand door je eigen golffunctie beschreven kan worden, omdat de golffuncties van alle andere mensen jouw golffunctie beïnvloeden, en de hele kamer zich in één gezamenlijke toestand bevindt. We willen weten hoe jij je gedraagt, maar om dat te doen moeten we eigenlijk ook het gedrag van alle andere mensen in de kamer bijhouden, wat voor meer dan twee of drie mensen in een kamer een heel moeilijke – en vaak zelfs een onmogelijke – berekening oplevert. Dit heet het N-deeltjesprobleem (“many body problem” in het Engels), en is een van de grootste struikelblokken voor het doen van nauwkeurige berekeningen in de quantummechanica.
Een quasideeltje
Kijk eens om je heen; alles in je directe omgeving bestaat niet uit een of twee, maar uit miljarden deeltjes. Een korreltje tafelzout bestaat al uit ongeveer 1018 atomen (oftewel 1.000.000.000.000.000.000 atomen), dus je kunt je voorstellen (of beter gezegd: helemaal niet voorstellen) hoeveel er wel niet in je mobiele telefoon zitten, of in je computerscherm! Toch willen we als natuurkundigen begrijpen wat er gebeurt wanneer er, bijvoorbeeld, een elektron door zo’n zoutkorrel beweegt.
Zo’n zoutkorrel bestaat uit een rooster van positief geladen natrium-ionen, en negatief geladen chloor-ionen. De negatieve lading van het elektron trekt de natrium-ionen aan en stoot de chloor-ionen af, waardoor het rooster verstoord wordt, zoals in afbeelding 2.
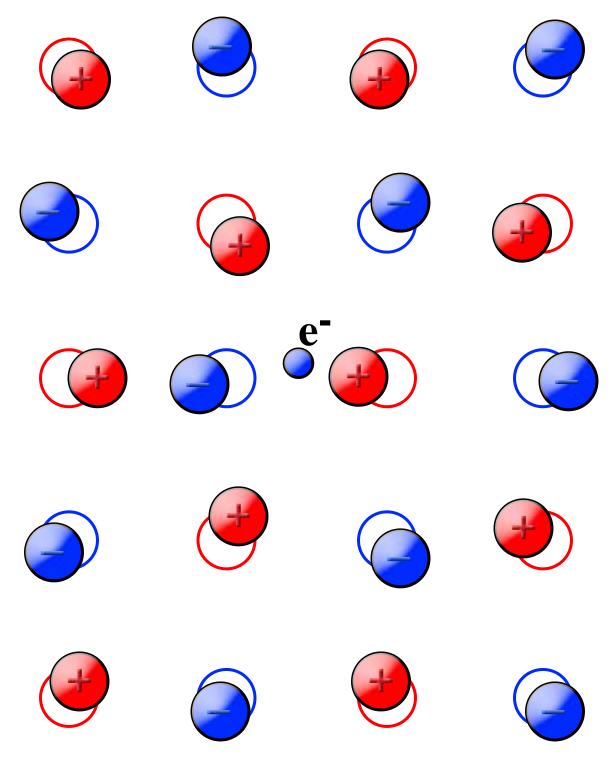
Afbeelding 2. Een elektron in een zoutkorrel. Een elektron in een ionisch rooster trekt de positief geladen ionen naar zich toe, en duwt de negatief geladen ionen van zich weg. Zo zorgt het elektron voor verplaatsingen van heel veel van de ionen in het rooster. Afbeelding: Wikipediagebruiker S_klimin.
De ‘kamer’ die we nu beschrijven, is dus gevuld met ionen in een rooster-opstelling plus een elektron, en de wisselwerkingen tussen die twee zorgen ervoor dat de beweging van één deeltje in het systeem alle andere deeltjes beïnvloedt. De boekhouding van de exacte oplossing is moeilijk bij te houden, maar de Rus Lev Landau bedacht daar in 1933 een simpele oplossing voor. We weten namelijk dat de wisselwerking tussen het elektron en het rooster ervoor zorgt dat het elektron zich moeilijker voortbeweegt. In plaats van alle bewegingen van alle ionen en het elektron mee te nemen, bedacht Landau dat we net zo goed kunnen doen alsof de ionen wél gewoon stilstaan, maar het elektron nu niet massa me heeft, maar een grotere massa, m*, waardoor het moeilijker vooruitkomt. Wat we nu beschreven hebben, wordt een elektron-quasideeltje genoemd. We gebruiken hier het Latijnse quasi, wat ‘alsof’ of ‘bijna’ betekent, want het deeltje gedraagt zich bijna als een gewoon elektron, maar dan met een iets andere massa.
Een trillend rooster
Een kristalrooster kan, zelfs zonder een loslopend elektron erin, nog allerlei andere soorten verstoringen hebben, waarbij we ook niet de details van ieder individueel deeltje willen bijhouden om het gedrag van het systeem te kunnen beschrijven. Denk bijvoorbeeld aan trillingen in het rooster. In de grondtoestand (de toestand met de laagst mogelijke energie) staan in een vaste stof alle deeltjes – atomen of ionen – helemaal stil. Als we nu een geluidsgolf door het materiaal heen sturen, beginnen de deeltjes heen en weer te bewegen, zoals bijvoorbeeld in afbeelding 3.

Afbeelding 3. Geluidsgolven in een vaste stof. Verschillende manieren waarop een 1-dimensionaal rooster van atomen kan trillen. De trillingen zijn niet op schaal: in een echt kristal zouden de verschuivingen wel veel kleiner zijn. Afbeelding: Wikipediagebruiker Greg L.
Het interessante is nu dat de energie van trillingen in een rooster gequantiseerd is, dus alleen maar een bepaald aantal vaste waardes kan aannemen, net zoals dat bijvoorbeeld geldt voor de energieniveaus van elektronen rondom een atoomkern. Om het gedrag van deze trillingen te beschrijven, kunnen we doen alsof we, beginnend met de grondtoestand zonder trillingen, per trillingswijze één ‘trillingsdeeltje’ toevoegen aan het systeem, een zogeheten fonon. (Niet te verwarren met het ‘foton’, een lichtdeeltje!) Technisch gezien is zo’n fonon niet echt een deeltje, maar een collectieve excitatie van de deeltjes in het systeem. Door het systeem zo te beschrijven kunnen we echter, net zoals met elektron-quasideeltjes, het gedrag van een gecompliceerd systeem dat uit heel veel (wisselwerkende) deeltjes bestaat, eenvoudig begrijpen en doorrekenen.
Topje van de ijsberg
We hebben nu twee voorbeelden gezien van soorten quasideeltjes – ‘verzwaarde’ elektronen en fononen – maar vastestoffysici hebben er nog veel meer bedacht. We zullen die in dit artikel niet allemaal beschrijven, maar deze quasideeltjes hebben mooie namen als magnonen, plasmonen, plasmaritonen, excitonen, rotonen, skyrmionen, spinonen, Majorana-fermionen, en nog veel meer. De Cooperparen die in een supergeleider voorkomen en die we al eens eerder op deze site bespraken zijn ook quasideeltjes, en sommige materialen hebben zelfs quasideeltjes die beschreven kunnen worden als magnetische monopolen. Deze deeltjes gedragen zich dus als losse noord- of zuidpolen van magneten, waar zulke polen in de gewone natuur altijd in paren voorkomen!
Je ziet: vaste stoffen hebben veel te bieden hebben qua interessante (en soms zelfs ‘verboden’) natuurkunde, en quasideeltjes zijn allesbehalve standaard.