Symmetrieën en behoudswetten
In de natuurkunde zijn symmetrieën ontzettend belangrijk – zie bijvoorbeeld deze artikelen van Jorrit Kruthoff als je meer over dit onderwerp wilt weten. Bij het oplossen van bijna alle natuurkundige problemen wordt gebruik gemaakt van symmetrie. Eén belangrijk gevolg van symmetrieën in de natuur is het bestaan van behoudswetten, zoals de wet van energiebehoud. Omdat energie altijd behouden is, kan je bijvoorbeeld de snelheid berekenen van een bal die je van een bepaalde hoogte hebt laten vallen, op het moment dat die bal de grond bereikt. Maar ook kan aan de hand van energiebehoud berekend worden welke deeltjes er kunnen ontstaan na een bepaalde botsing in een deeltjesversneller. Er zijn ook heel eenvoudige vragen en puzzels die je op kan lossen met behulp van een behoudswet. Hier volgt een voorbeeld.
Puzzel 1:
We nemen twee emmers die beide 5 liter verf bevatten. Één emmer met witte en één emmer met groene verf, zoals te zien in afbeelding 1.
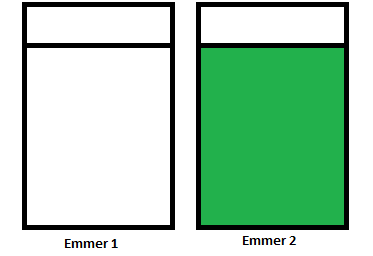
Afbeelding 1. De beginsituatie.Emmer 1 (links) bevat 5 liter witte verf; emmer 2 (rechts) 5 liter groene verf.
Nu doen we het volgende: eerst gooien we een beker witte verf uit emmer 1 bij de groene verf uit emmer 2, en mengen de verf in die emmer goed. Het eindresultaat is als volgt:
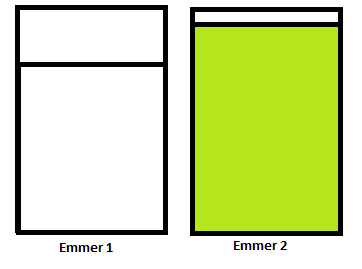
Afbeelding 2. De tussenstap.Een beker verf uit de linkeremmer is aan de rechteremmer toegevoegd.
Vervolgens gooien we een beker uit de (nu gemengde) emmer 2 bij de witte verf uit emmer 1.
Vraag: Welke emmer bevat er nu méér kleur van de ander?
De mogelijke antwoorden zijn natuurlijk:
- Emmer 1: Er zit meer groene verf in emmer 1 dan witte verf in emmer 2.
- Emmer 2: Er zit meer witte verf in emmer 2 dan groene verf in emmer 1
- Beiden emmers bevatten evenveel verf van de andere kleur.
Denk eerst even na over het antwoord voordat je verder leest!
Je zou misschien intuïtief verwachten dat antwoord b het juiste antwoord is – dat was in elk geval mijn eigen eerste gok. We hebben immers een volledige beker witte verf in emmer 2 gegooid, terwijl de beker uit emmer 2 ook wat witte verf bevatte toen we hem in emmer 1 gooiden.
Dit is echter niet waar! Het enige juiste antwoord is c. Beide emmers bevatten evenveel verf van de andere kleur. Dit kunnen we begrijpen met behulp van het feit dat zowel de totale hoeveelheid groene als de totale hoeveelheid witte verf ‘behouden grootheden’ zijn, net als energie.
Ten eerste is het namelijk zo dat de hoeveelheid verf in beide emmers na het uitvoeren van de twee stappen weer precies gelijk is aan 5 liter. Ook weten we dat de hoeveelheid witte en groene verf allebei behouden grootheden zijn. Er is geen groene verf veranderd in witte of omgekeerd, en er is ook geen verf verdwenen of extra ontstaan. Dit klinkt natuurlijk ontzettend logisch, maar het is precies de eigenschap die we nodig hebben. Het betekent namelijk, dat alle witte verf die niet meer in emmer 1 zit, nu in emmer 2 zit, en vice versa. Omdat de hoeveelheid verf in beide emmers hetzelfde is, moet de hoeveelheid groene verf in emmer 1 wel gelijk zijn aan de hoeveelheid witte verf in emmer 2!
Ongelooflijke kracht van eenvoudige wiskunde
In de natuurkunde is intuïtie vaak erg belangrijk. Als er iets wordt uitgerekend, is het heel nuttig om aan de hand van je intuïtie na te gaan of dit het antwoord is dat je zou verwachten, en waarom dan wel of niet. Soms is onze intuïtie echter helemaal verkeerd, zelfs in gevallen waar je het antwoord met heel eenvoudige wiskunde kan checken. Hier volgt een voorbeeld van zo’n opgave.
Puzzel 2:
Stel je eens voor dat we de aarde een riem om doen. Een heel lange riem, die precies rondom de evenaar past. Nu nemen we deze riem, maken hem één meter langer, en binden hem opnieuw rondom de evenaar. De riem is nu natuurlijk iets te groot, en we gaan ervanuit dat hij overal rondom de aarde precies even hoog boven de evenaar ‘zweeft’. De vraag is nu: hoe hoog komt de riem?
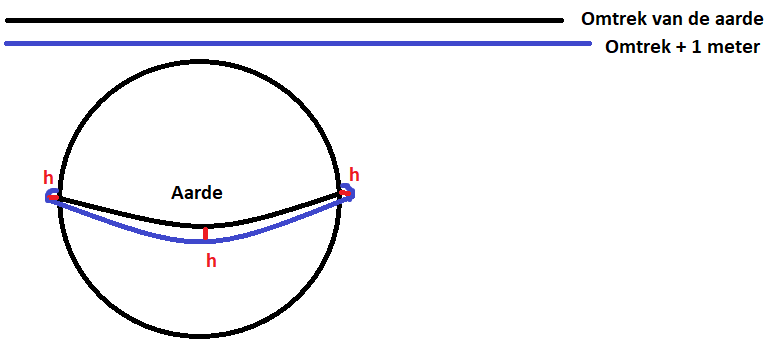
Afbeelding 3. De aarde met een riem om.De riem (blauw) is 1 meter langer dan de omtrek van de aarde (zwart).
Voor we dit berekenen kan het geen kwaad om het antwoord eerst te gokken.
Doe dit weer voordat je verder leest.
Ik zou zelf gegokt hebben dat, omdat de aarde zo enorm groot is, en we er maar een meter bij hebben geplakt, de riem maar een héél klein beetje boven de aarde uitsteekt. Misschien in de orde van grootte van een millimeter?
Nu laten we de wiskunde spreken. De straal van de aarde noemen we R en de straal van de riem noemen we r. We zijn dan op zoek naar de hoogte h = r − R.
De omtrek van de aarde is O = 2·π·R en de lengte van de riem is L = 2·π·r = O + 1. Als we dit combineren, zien we dat
h = r − R = (O+1) / 2π – O / 2π = 1 / 2π ≈ 0,16 m
Ik weet niet hoe het voor jullie voelt, maar dit antwoord is veel groter dan ik had verwacht!
Nog een bonusvraag: wat gebeurt er als we de riem straktrekken naar één kant? Hoe hoog kan hij dan maximaal komen? Deze situatie is te zien in afbeelding 4. Wat denk je dat de hoogte h nu is?
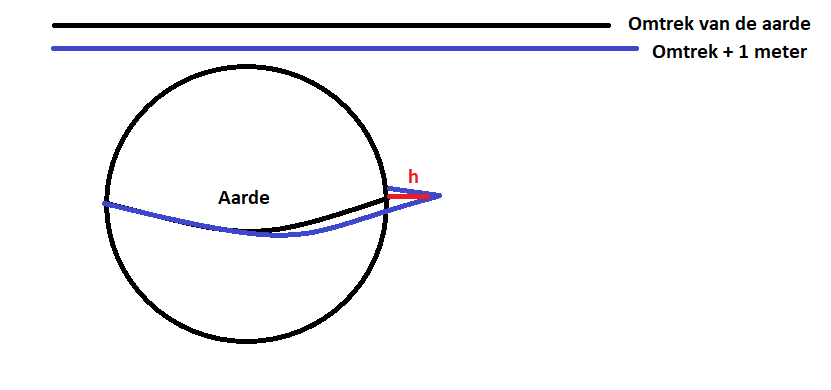
Afbeelding 4. Nogmaals de aarde met een riem om.Nu is de riem strakgetrokken naar één kant.
Met bijna even eenvoudige wiskunde (probeer het zelf eens!) kan je laten zien dat de gezochte hoogte maar liefst 121 meter is. Opnieuw sta ik versteld.
Zwaartekrachtlenzen

Afbeelding 5. Een zwaartekrachtlens.De lenswerking van een zwart gat dat voor een groot sterrenstelsel langs beweegt. Animatie: Urbane Legend.
Het fenomeen van zwaartekrachtlenzen is op deze site al eerder beschreven, bijvoorbeeld in dit artikel. Het blijkt dat de zwaartekracht in het heelal soms op kan treden als een lens. Stel dat we vanaf de aarde kijken naar een sterrenstelsel heel ver weg, dan kan het zijn dat zich in de tussenliggende ruimte andere zware objecten bevinden, zoals zwarte gaten. En zoals Einstein ons heeft geleerd: zware objecten zorgen ervoor dat de ruimte krom wordt. Als de ruimte gekromd is, betekent dat ook dat lichtstralen niet meer in rechte lijnen bewegen, maar afbuigen, net als in een lens gebeurt. Door deze lenswerking kan het zijn dat we het sterrenstelsel niet één keer zien, maar meerdere keren, zoals te zien in de foto in afbeelding 6 hieronder. Dit verschijnsel wordt ook wel een Einsteinkruis genoemd. De vier felle stippen die je ziet zijn allemaal afbeeldingen van hetzelfde sterrenstelsel.
Er zijn inmiddels heel veel mooie foto’s te vinden van sterrenstelsels die je meerdere keren ziet. Wat nu opvalt, is dat dit altijd een even aantal keer is. We zien altijd twee, vier of bijvoorbeeld zes keer hetzelfde, maar nooit drie of vijf.

Afbeelding 6. Een Einsteinkruis.De vier felle stippen zijn allemaal beelden van hetzelfde sterrenstelsel.
Puzzel 3:
De vraag is nu: hoe komt het dat je altijd een even aantal van deze afbeeldingen ziet?
Deze vraag is, in tegenstelling tot de voorgaande vragen, een stuk moeilijker te beantwoorden. Maar het blijkt dat je met eenvoudige wiskunde al wel heel ver komt.
Ten eerste moet gezegd worden dat er eigenlijk juist altijd een oneven aantal afbeeldingen is. Eén van deze afbeeldingen is echter altijd heel erg klein en valt precies weg achter het zware object dat voor de kromming van de ruimte zorgt. Er zijn dus maar een even aantal beelden te zien.
Een tekening van de situatie zonder dat de ruimte vervormd is, is te zien in afbeelding 7. Lichtstralen vanuit een sterrenstelsel gaan in een rechte lijn naar de aarde. We tekenen twee cirkels: een cirkel heel dichtbij het sterrenstelsel en nog een heel grote cirkel zo groot als de afstand tot de aarde. Al het licht van het sterrenstelsel zal eerst langs cirkel 1 komen en daarna aankomen bij cirkel 2. (In de praktijk zit er natuurlijk een bol om het sterrenstelsel heen, en geen cirkel, maar dat maakt voor de onderstaande redenering niet uit, en een cirkel is natuurlijk wel zo makkelijk te tekenen.)
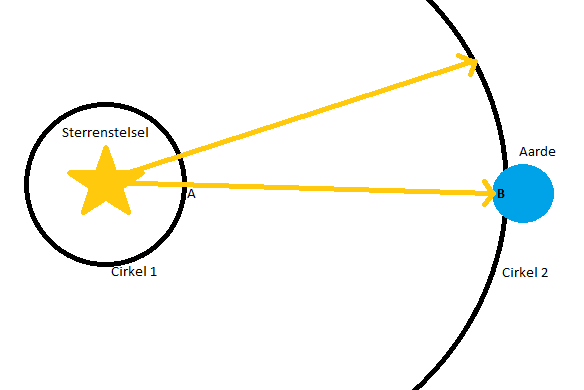
Afbeelding 7. Licht van een ver sterrenstelsel.Lichtstralen die van een ver sterrenstelsel naar de aarde komen. In deze situatie is de ruimte nog niet gekromd, en gaan de lichtstralen rechtdoor.
De redenering gaat nu als volgt. We zien dat elke lichtstraal maar één snijpunt heeft met cirkel 1 en dan rechtdoor straalt richting cirkel 2. Dit betekent dat we een functie F op kunnen stellen waarbij elk punt op cirkel 1 wordt afgebeeld op cirkel 2.
F(punt op cirkel 1) = punt op cirkel 2
Bijvoorbeeld: F(A) = B
Als we dus punt A in de functie stoppen, dan krijgen we punt B eruit. Op punt B op aarde zien we dus eigenlijk het licht dat eerst op punt A was.
Nu gaan we bekijken wat er gebeurt als er zich een heel zware massa tussen de aarde en het sterrenstelsel bevindt. Die massa zal ervoor zorgen dat de ruimte gaat krommen. Daarom gaan lichtstralen niet meer rechtdoor, maar zullen ze afgebogen worden. Wat blijkt nu: wiskundig kan je de situatie ook omdraaien. In plaats van de lichtstralen te vervormen, kunnen we precies hetzelfde resultaat krijgen als cirkel 1 vervormd wordt. Dit is te zien in afbeelding 8. Door de situatie op deze manier om te draaien, wordt het beantwoorden van onze vraag opeens mogelijk!
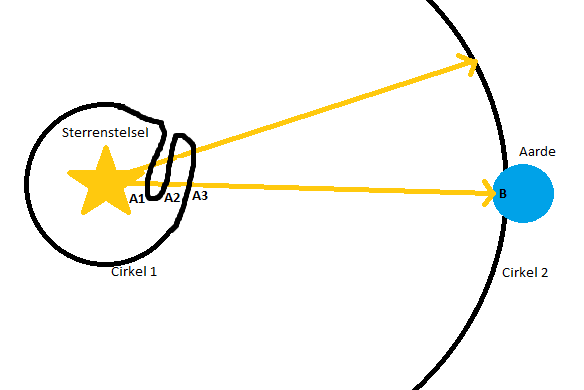
Afbeelding 8. Gekromde ruimte?In deze afbeelding is de gekromde ruimte weer ‘gladgemaakt’; het resultaat is dat de cirkel om het sterrenstelsel heen nu vervormd is.
Wat we nu zien, is namelijk dat de lichtstraal die naar de aarde gaat niet één maar drie snijpunten heeft met cirkel 1. Als de lichtstraal nu op aarde aankomt, kunnen we ons afvragen: van welke plek op cirkel 1 komt deze lichtstraal?
Er zijn dan drie antwoorden mogelijk:
F(A1) = B,
F(A2) = B,
F(A3) = B
Natuurkundig betekent dit dat je vanaf punt B drie beelden ziet: je zal het sterrenstelsel drie keer zien in plaats van één keer!
Nu rest het laatste deel van de vraag: waarom is het aantal beelden altijd oneven? Het antwoord is als volgt. Hoe meer de ruimte gekromd is, hoe meer cirkel 1 vervormd zal zijn. Dan zal het zwarte lijntje van cirkel 1 nog meer op en neer gaan. Maar hoe vervormd de cirkel ook is, de lichtstraal moet hem altijd een oneven aantal maal kruisen om uiteindelijk bij punt B aan te komen.Bij elke nieuwe keer “omhoog” hoort namelijk ook een nieuwe keer “omlaag”. Probeer maar eens een cirkel te tekenen waarbij dat niet zo is!
Zoals gezegd is bij een gekromde ruimte één van deze beelden nooit te zien. Het resterende aantal is dus even We hebben daarmee dus beredeneerd waarom er op foto’s van zwaartekrachtlenzen altijd een even aantal beelden te zien is!