
Afbeelding 1. Meting van een botsing in de Large Hadron Collider.Bij experimenten zoals die in de LHC in Genève is het vaak de theorie die moet proberen de precisie van de metingen te evenaren. Afbeelding: LHC/CERN.
In de deeltjesfysica beschrijven we de natuur in termen van de allerkleinste bouwstenen: de elementaire deeltjes. Het bestaan van en de interacties tussen al deze deeltjes worden getest door ze op elkaar te schieten met heel hoge energieën. In zogeheten deeltjesversnellers worden geladen deeltjes versneld met behulp van sterke elektrische velden om ze vervolgens op elkaar te laten botsen. Dit kunnen elementaire deeltjes zijn, maar ook grotere deeltjes die zelf weer bestaan uit deze kleinere bouwstenen. In de Large Hadron Collider op het CERN schieten onderzoekersbijvoorbeeld protonen op elkaar. Door de hoge energieën bestaat er een soort soep van elementaire deeltjes die ontzettend veel interacties met elkaar uitvoeren en uiteindelijk combineren tot zogeheten hadronen en leptonen die we in de detectoren meten[1]. Door dit zeer succesvolle experiment hebben we het standaardmodel, de theorie die de elementaire deeltjes en hun interacties beschrijft, tot op heel hoge precisie kunnen testen. Zo precies zelfs dat onze theoretische berekeningen tegenwoordig soms aan precisie te kort komen.
Nu denk je vast: ‘Huh? hebben theoretische berekeningen onzekerheden?’ Jazeker: dit zijn onzekerheden die verschijnen door de beperkingen van het model dat je gebruikt om de voorspellingen te maken. Vooralsnog komen de theoretische en de experimentele voorspellingen weliswaar overeen binnen de foutmarges, maar omdat we weten dat het standaardmodel niet compleet is (het beschrijft bijvoorbeeld geen zwaartekracht) willen we ook de theoretische onzekerheden verkleinen. Vooral omdat er processen zijn waar bepaalde spanningen tussen meting en voorspelling bestaan, hopen we op deze manier de verschillen tussen meting en theorie te ontdekken.
Effectieve theorieën
Om steeds betere voorspellingen te doen die ons helpen om te kijken of het standaardmodel ons de juiste informatie verschaft, hebben we ook steeds nieuwe rekentechnieken nodig. Aangezien het standaardmodel nogal ingewikkeld is, kunnen we proberen zogeheten effectieve theorieën op te stellen. Diemaken het mogelijk om ingewikkelde (lees: vooralsnog onmogelijke) berekeningen toch uit te voeren, maar niet zonder prijs: in ruil daarvoor krijgen we theoretische onzekerheden.
Laten we eerst kijken wat een effectieve theorie opstellen werkelijk inhoudt. Hiervoor is het inzichtelijk om terug te gaan naar een theorie die Enrico Fermi in de jaren 30 bedacht om het bètaverval te verklaren. Onder bètaverval verstaan we radioactief verval van atoomkernen door middel van het uitstralen van een elektron of positron. Om dit proces te kunnen verklaren introduceerde Fermi een interactie die kon plaatsvinden tussen vier leptonen. Deze interactie verklaarde het bètaverval van een neutron door een directe koppeling met een elektron, een neutrino (later werd duidelijk dat dit een anti-neutrino was) en een proton zoals in afbeelding 2.
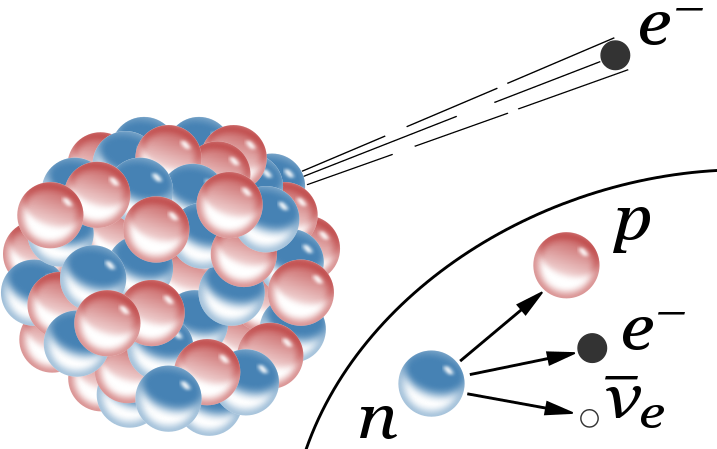
Afbeelding 2. Bètaverval.Bètaverval in een atoom door middel van een vierpuntsinteractie tussen neutron, proton, elektron en anti-neutrino. Afbeelding: Wikipedia.
Deze verklaring was een voorloper van de huidige theorie van de zwakke kernkracht, waarin het verval van het neutron wordt verklaard door een intermediair deeltje: het W-boson, een elementair deeltje uit het standaardmodel. Protonen en neutronen zijn hadronen, wat wil zeggen dat ze ieder uit quarks bestaan. Een down-quark kan een W-boson uitzenden en zo in een up-quark veranderen. Omdat down-type quarks een negatieve en up-type quarks een positieve elektrische lading hebben, gaat de verandering via een negatief geladen W–-boson, zodat de totale elektrische lading behouden is. Een W–-boson vervalt op zijn beurt in een lepton en een neutrino uit dezelfde familie, waarbij de bijdrage van verval naar elektron + elektronneutrino het grootst is. In afbeelding 3 is schematisch afgebeeld hoe de zwakke kracht het neutron in een proton verandert.
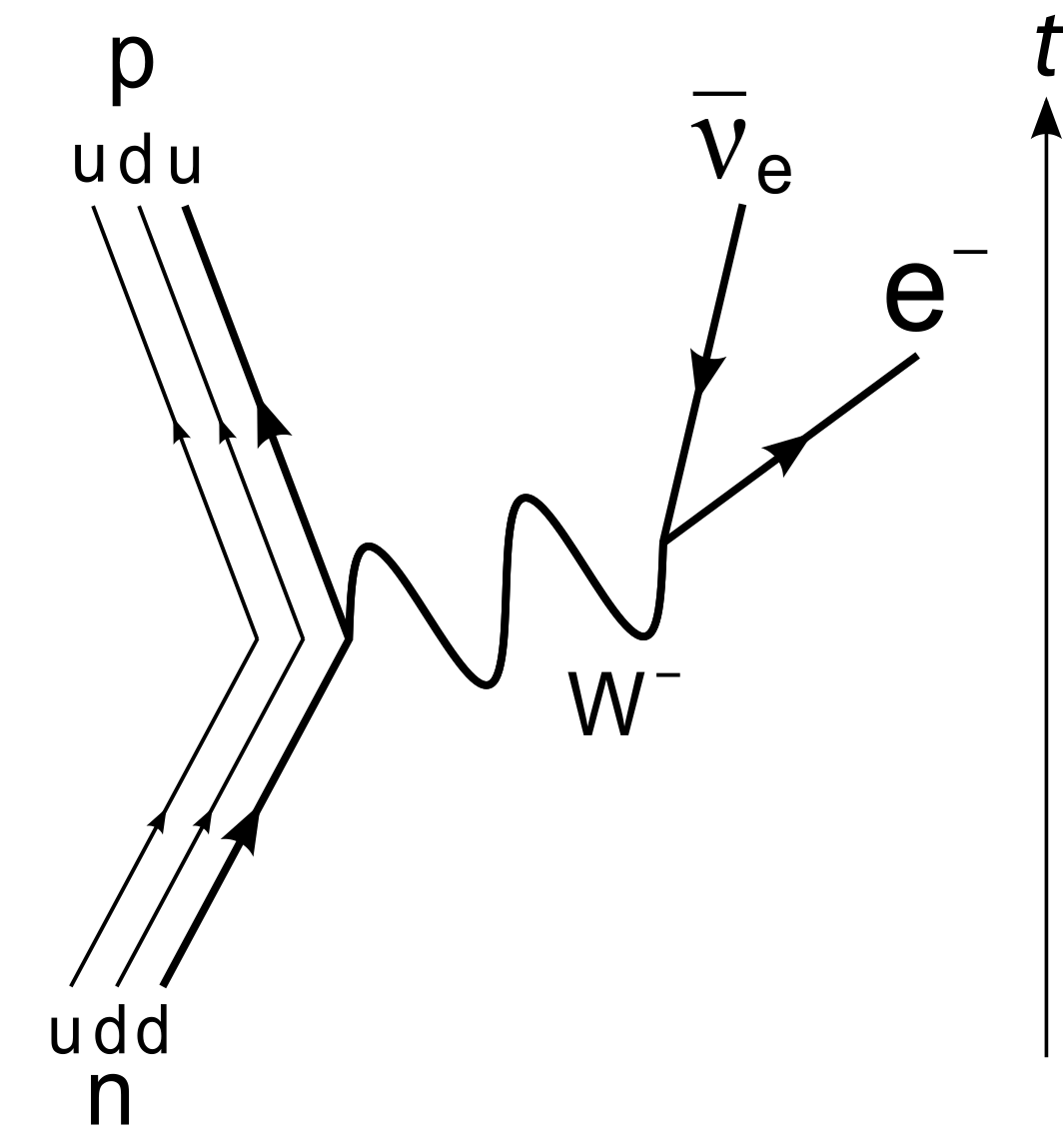
Afbeelding 3. Verval van een neutron.Verval van een neutron veroorzaakt door zwakke interactie. Afbeelding: Wikipedia.
Rekenen aan versnellers
Achteraf, nu we weten dat bètaverval via het uitzenden van een W-boson gaat, kunnen we Fermi’s theorie beschouwen als een effectieve theorie. Voorspellingen met behulp van Fermi’s vierpunt-interactie zijn vele malen makkelijker dan die met behulp van de echte elementaire deeltjes, en geven toch een zeer accurate weergave van de werkelijkheid. Dit alles is het gevolg van een scheiding van energie-schalen, wat de belangrijkste overweging is bij het opstellen van een effectieve theorie. In het geval van Fermi’s theorie betekent dit dat we weg moeten blijven van energieën dichtbij de massa van het W-boson; voor processen met kleinere energie voldoet Fermi’s beschrijving uitstekend.
Om de uitkomsten van processen die plaatsvinden in deeltjesversnellers te voorspellen kunnen we ook een effectieve theorie opstellen. We gebruiken de scheiding van energieschalen dan om deeltjes met verschillende energie en richting te onderscheiden. Om preciezer te zijn willen we de zachte interacties (dus die tussen deeltjes die weinig energie hebben), de collineaire interacties (die tussen deeltjes die in dezelfde richting bewegen) en de harde interacties (die tussen deeltjes met veel energie die niet in dezelfde richting bewegen) van elkaar onderscheiden. Dit wordt gedaan in de zogeheten SCET: Soft-Collinear Effective Theory. De theoretische onzekerheden in deze theorie komen van de energie waarop het verstrooiingsproces van de botsing plaatsvindt en van de meting die wordt uitgevoerd op de deeltjes die in de detectoren vliegen. Deze twee factoren vertellen namelijk hoe goed onze effectieve theorie nu eigenlijk is. In feite voorspellen de theoretische onzekerheden hoe groot de correcties zijn op onze aanname dat zachte, collineaire en harde interacties zich op een andere energieschaal bevinden.
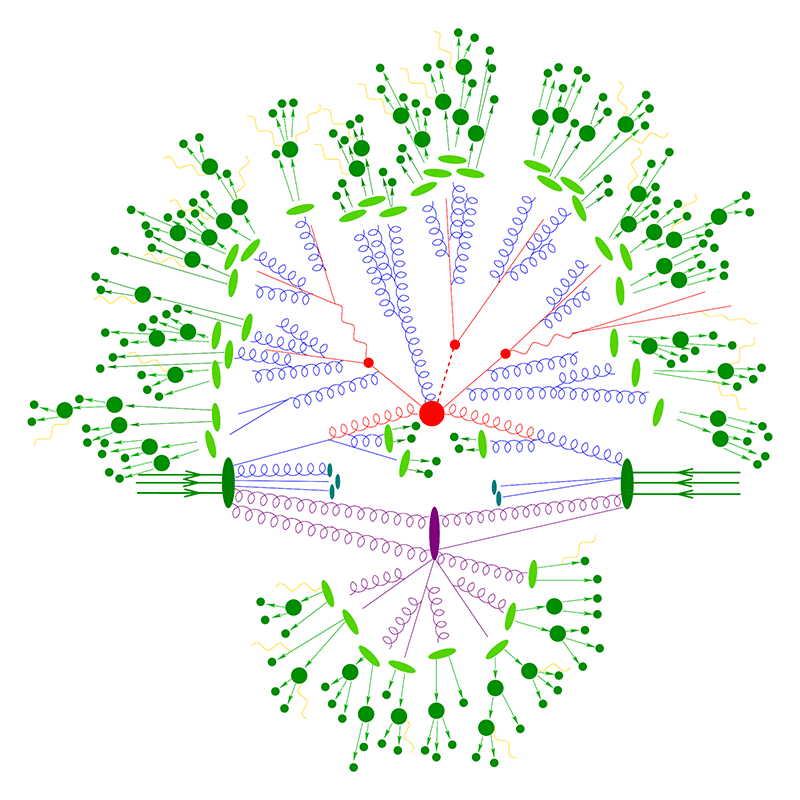
Afbeelding 4. Een botsing in de LHC.Grafische weergave van een botsing tussen twee protonen in de LHC. Afbeelding: SLAC – Stanford University.
Factoriseren en hersommeren
Door gebruik te maken van SCET kunnen we de verstrooiing van een botsing beschrijven door middel van losse ingrediënten: zachte interacties, collineaire interacties en harde interacties. We noemen dit factorisatie, aangezien we het gehele proces gefactoriseerd hebben, opgebroken, in deelprocessen[2]. De zachte en collineaire interacties zijn theoretisch moeilijke processen om aan te rekenen. Dit komt doordat zachte deeltjes vrijwel geen energie hebben en daardoor niet worden gemeten door de detectoren van de deeltjesversneller. Of je nu één zacht deeltje of duizend hebt, maakt dus geen verschil voor de meting. Hetzelfde geldt voor collineaire interacties. Aangezien detectoren een bepaalde resolutie hebben en collineaire deeltjes allemaal precies dezelfde richting op gaan, kan de detector niet uitmaken of het één heel energiek deeltje meet of meerdere collineaire deeltjes. In theorie kun je dus oneindig veel zachte en collineaire interacties toevoegen om hetzelfde proces te beschrijven, en dat is duidelijk een probleem…
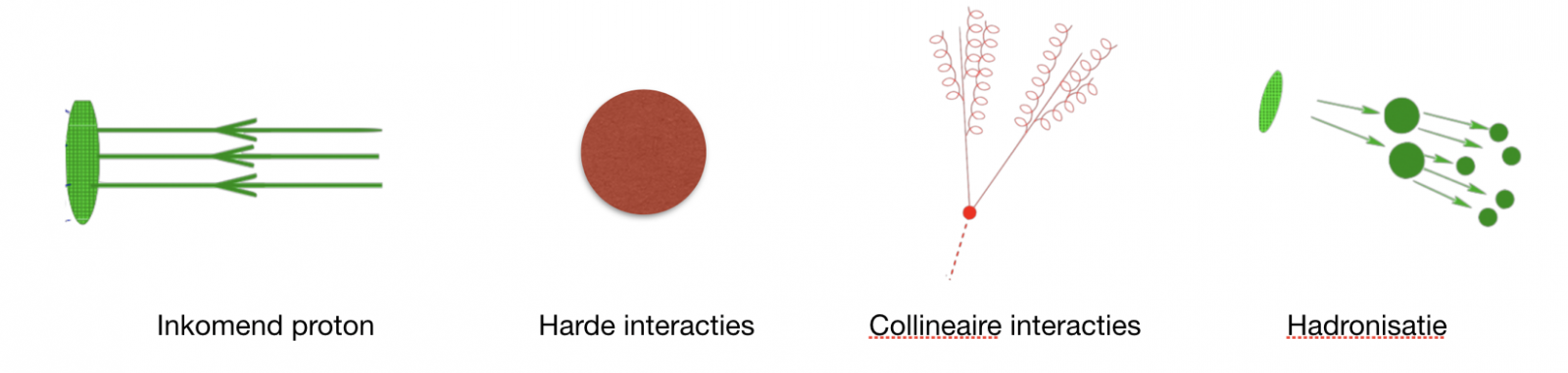
Afbeelding 5. Factorisatie.De verschillende soorten processen die in de factorisatie van een botsing zoals in afbeelding 4 een rol spelen.
Alle ingrediënten die in de factorisatie voorkomen hangen af van de energie waarop de botsing plaatsvindt. Een bijkomstig resultaat is dat alle ingrediënten een eigen energieschaal hebben waarop bepaalde onrealistische oneindig grote bijdrages voor dit specifieke ingrediënt uit de berekeningen verdwijnen, een schaal die ook wel de natuurlijke schaal wordt genoemd. Als we de zachte, collineaire en harde bijdrages op hun natuurlijke schaal uitrekenen geven ze dus een realistische, eindige bijdrage aan het volledige proces. Aangezien de daadwerkelijke botsing maar op één energie plaatsvindt moeten we achteraf wel alles omrekenen naar dezelfde energie. Dit laatste heet hersommatie, en dankzij deze hersommatie heeft deze techniek een voorspellende gave voor alle zachte en collineaire straling.
De strijd om als eerst een discrepantie tussen experiment en het standaardmodel te vinden is dankzij de bovenstaande technieken losgebarsten. Of zal een dergelijke afwijking nooit gevonden worden? Misschien, maar hoe verklaren we dan de fenomenen die niet door het standaardmodel worden uitgelegd, zoals donkere materie, donkere energie en baryon-asymmetrie? De toekomst zal het leren…