Ruimte, tijd en zwaartekracht bestaan op de allerkleinste schaal niet. Nieuwe inzichten in de theoretische natuurkunde lijken althans tot die verrassende conclusie te leiden. Op macroscopische schaal komen deze alledaagse verschijnselen als ‘emergente’ effecten uit de microscopische fysica tevoorschijn. Natuurkundige Erik Verlinde presenteert vandaag zijn nieuwe theorie van emergente zwaartekracht, die de huidige zwaartekrachtswetten van Newton en Einstein aanpast. Zijn theorie verklaart zowel de versnelde uitdijing van het heelal – veroorzaakt door donkere energie – als de extra zwaartekracht die onder meer wordt waargenomen aan de rand van sterrenstelsels, en die normaliter wordt toegeschreven aan de mysterieuze ‘donkere materie’.
Door Manus Visser en Marcel Vonk

Afbeelding 1. Erik Verlinde.In zijn artikel ‘Emergent gravity and the dark universe’ presenteert de UvA-onderzoeker vandaag zijn nieuwste inzichten in het gedrag van de zwaartekracht.
- Drie zwaartekrachtraadsels
- Een uitweg: emergente zwaartekracht
- Zwaartekracht uit informatie
- Entropie en oppervlakte
- Positief en negatief gekromde ruimte
- Donkere energie: een volumebijdrage aan de entropie
- Het ontstaan van gewone materie
- Een formule voor donkere materie
- Conclusie
Drie zwaartekrachtraadsels
De zwaartekracht houdt ons met beide benen op de grond. Ze zorgt ervoor dat de aarde grofweg bolvormig is, en dat onze planeet in een baan rond de zon draait. Zonder zwaartekracht zou onze wereld er totaal anders uitzien. Toch is het van de vier fundamentele natuurkrachten juist de zwaartekracht die natuurkundigen het minst goed begrijpen.
Er zijn maar liefst drie grote problemen met ons begrip van de zwaartekracht. Ten eerste begrijpen we niet goed hoe die kracht zich op de allerkleinste schaal gedraagt. Het combineren van de quantummechanica met de algemene relativiteitstheorie levert beruchte oneindigheden op, die erop wijzen dat we de wetten van Einstein niet zomaar kunnen toepassen op subatomair niveau. Dit conflict staat bekend als het probleem van de quantumzwaartekracht.
Het tweede probleem vindt zijn oorsprong in een kosmologische waarneming. In 1998 kwamen twee onafhankelijke teams van astronomen tot de conclusie dat ons heelal versneld uitdijt. Die ontdekking kwam voor veel natuurkundigen als een grote verrassing. Zwaartekracht is immers een aantrekkende kracht, die de uitdijing van het heelal juist zou moeten afremmen! Om de extra afstoting te kunnen verklaren, moest men aannemen dat het heelal een gigantische hoeveelheid extra energie bevat. Die energie, ook wel donkere energie genoemd, kan gezien worden als de energie van het vacuüm zelf. De mysterieuze donkere energie vormt maar liefst 69 procent van de totale hoeveelheid energie in het heelal.
Het derde probleem rond de zwaartekracht werd in het begin van de jaren ’30 ontdekt door Jan Oort en Frits Zwicky, en kreeg in de jaren ’60 en ’70 een revival door waarnemingen van Vera Rubin en Kent Ford. Deze astronomen zagen dat de snelheid waarmee sterren aan de rand van sterrenstelsels rond het centrum draaien, veel groter is dan op grond van de zichtbare materie in die sterrenstelsels zou worden verwacht. Iets soortgelijks geldt voor de snelheden waarmee de sterrenstelsels zelf rond het centrum van een cluster van zulke stelsels draaien. Volgens Newtons zwaartekrachtstheorie vermindert de snelheid waarmee verre objecten rond een grote massaconcentratie draaien naarmate de afstand tot het centrum toeneemt. Astronomen namen echter waar dat de rotatiesnelheden in de buitengebieden van veel sterrenstelsels en clusters juist gelijk blijven of zelfs stijgen! Ondanks die hoge snelheden vliegen dergelijke sterren en sterrenstelsels niet uit hun baan. Er wordt dus kennelijk harder aan ze getrokken dan men op basis van de zichtbare massa zou verwachten. Waar komt deze extra aantrekkingskracht vandaan?
De meeste onderzoekers schrijven de extra zwaartekracht uit dit derde probleem toe aan donkere materie – materie die zou bestaan uit vooralsnog onbekende deeltjes. Ook hier gaat het weer om een enorm groot effect: er zou in het universum ongeveer vijf keer zo veel donkere materie moeten bestaan als gewone, zichtbare materie. Daarmee is nog eens 26 procent van de inhoud van het heelal onbekend; op zijn zachtst gezegd een onbevredigende situatie. Er wordt momenteel dan ook veel onderzoek gedaan om de deeltjes waaruit donkere materie zou bestaan direct of indirect waar te nemen.
De nieuwe theorie van Erik Verlinde voorspelt echter dat de experimenten zulke deeltjes niet zullen vinden. Volgens hem heeft de extra aantrekkingskracht in de buitengebieden van sterrenstelsels een totaal andere oorsprong.
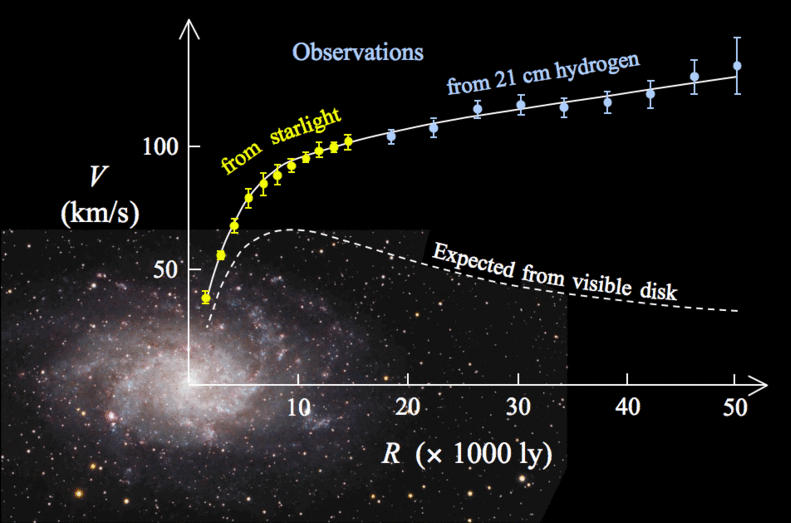
Afbeelding 2. Draaisnelheden van sterren in een sterrenstelsel.Volgens Newtons zwaartekrachtswetten zouden sterren in de buitengebieden van sterrenstelsels langzamer moeten gaan bewegen naarmate de afstand tot de kern groter wordt. (Gestippelde lijn.) In de praktijk wordt echter waargenomen dat de snelheid gelijk blijft of, zoals in dit geval, zelfs toeneemt. (Doorgetrokken lijn.) Afbeelding: Stefania Deluca.
Een uitweg: emergente zwaartekracht
Hoe moeten we de problemen van quantumzwaartekracht, donkere materie en donkere energie te lijf gaan? Omdat al deze vraagstukken over de aard van de zwaartekracht gaan, is het niet uitgesloten dat ze uiteindelijk met elkaar te maken hebben. Wellicht moeten we ons beeld van de zwaartekracht zelf op fundamenteel niveau wijzigen, en werpt dat een licht op alle problemen tegelijk. Dat is precies wat Erik Verlinde met zijn nieuwe theorie hoopt te bewerkstelligen.
Verlindes ideeën bouwen voort op ontwikkelingen in de natuurkunde van zwarte gaten en de snaartheorie. Al in de jaren ’70 ontdekten Stephen Hawking, Jacob Bekenstein en anderen dat de fysica van zwarte gaten verrassend goed beschreven kan worden met natuurwetten die afkomstig zijn uit de thermodynamica. Daardoor kwamen natuurkundigen al snel tot de conclusie dat zwaartekracht – in elk geval rond zwarte gaten – een thermodynamisch verschijnsel is.
Thermodynamica gaat over macroscopische verschijnselen, zoals warmte en druk, die ontstaan uit microscopische natuurkunde. Denk aan de temperatuur van een kop koffie, die voortkomt uit de bewegingen van talloze individuele moleculen. Thermodynamische eigenschappen als temperatuur en druk bestaan op het allerkleinste niveau niet, maar zijn emergent en worden pas op macroscopische schaal zichtbaar. De relatie tussen thermodynamica en zwaartekracht suggereert dat ook zwaartekracht – en zelfs ruimte en tijd – op de allerkleinste schaal niet bestaat, en pas op grotere schaal tevoorschijn komt.
Dit idee van zwaartekracht als emergente kracht biedt een elegante oplossing voor het probleem van quantumzwaartekracht. Zwaartekracht bestaat immers niet op quantumniveau, dus we hoeven überhaupt niet op zoek naar wetten die de relativiteitstheorie met de quantumfysica verenigen! Verlindes nieuwe inzicht is dat emergente zwaartekracht ook de andere twee vraagstukken – donkere energie en donkere materie – kan oplossen. Om te kunnen begrijpen hoe dat gebeurt, moeten we terug naar wat natuurkundigen in navolging van Bekenstein en Hawking hebben ontdekt over de herkomst van de zwaartekracht.
Zwaartekracht uit informatie
Wat zijn de ‘atomen’ van de ruimtetijd? In een kop koffie zorgt het trillen van de allerkleinste bouwstenen – atomen en moleculen – ervoor dat de koffie warm is. Om de zwaartekracht ook als thermodynamisch effect te begrijpen, moeten we op zoek naar de bouwstenen van de ruimte om ons heen. In de afgelopen decennia hebben veel fysici zich met deze vraag beziggehouden.
Een belangrijke les uit die studie is dat het uiteindelijk niet eens zo heel veel uitmaakt hoe de atomen van de ruimtetijd er precies uitzien. Vergelijk het weer met de kop koffie: om de thermodynamische eigenschappen van koffie te begrijpen, hoeven we niet te weten uit welk soort moleculen de koffie bestaat, of hoe de atomen in die moleculen precies gerangschikt zijn. Veel belangrijker is het totale aantal moleculen, of de vraag welke bewegingsvrijheden die moleculen hebben. Met andere woorden: we zijn geïnteresseerd in de informatie die de moleculen met zich meedragen. Voor de zwaartekracht is de situatie hetzelfde: in zekere zin kunnen we de informatie zélf zien als de fundamentele bouwsteen.
In de quantumfysica gedraagt informatie zich echter anders dan we gewend zijn. In de klassieke natuurkunde is het zo dat één eenheid van informatie zich altijd op één bepaalde plaats bevindt. De ‘computerbits’ van de klassieke natuurkunde zijn de eigenschappen van individuele deeltjes, die zich op duidelijk gedefinieerde locaties bevinden. In de quantummechanica kan informatie echter ook gedeeld worden door verschillende deeltjes – een fenomeen dat bekend staat onder de naam verstrengeling. Informatie kan bijvoorbeeld verstopt zitten in een deeltjespaar, waarvan de ene helft zich hier op aarde, en de andere helft zich op de maan bevindt. Quantuminformatie is niet gelokaliseerd!
De laatste jaren hebben theoretisch fysici zich massaal gestort op het begrijpen van de gevolgen van deze verstrengeling. Het beeld dat daarbij ontstaan is, is dat ruimte en tijd op quantumniveau volledig bestaan, en in zekere zin zelfs ontstaan, uit niet-lokale informatie. Hoe kunnen we die nogal science-fictionachtig klinkende uitspraak begrijpen?
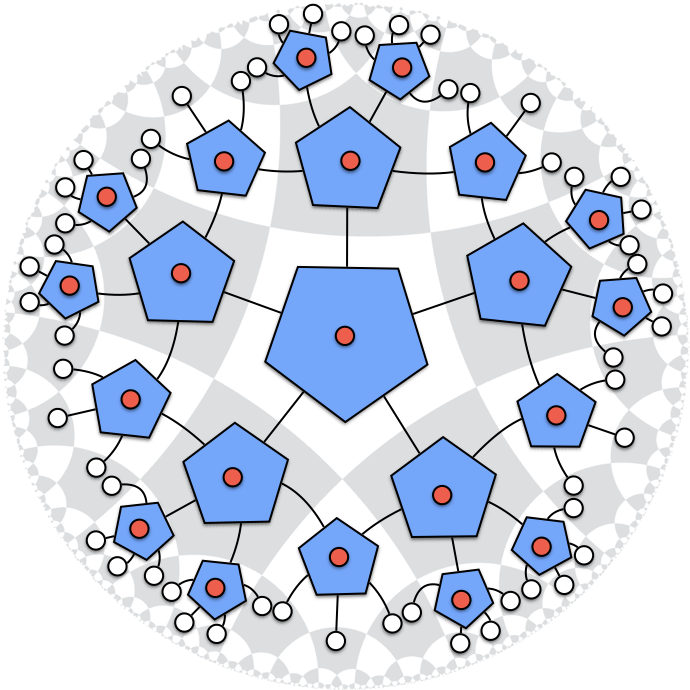
Afbeelding 3. Verstrengeling en informatie.Om de verdeling van informatie over de ruimte en de manier waarop die informatie verstrengeld is weer te geven, maken natuurkundigen gebruik van zogeheten ’tensornetwerken’. Hierboven een eenvoudig voorbeeld van zo’n netwerk; elk rondje is een quantumbit, en de lijntjes geven de verstrengeling tussen de verschillende bits aan. Afbeelding afkomstig uit ‘Holographic quantum error-correcting codes’ van F. Pastawski, B. Yoshida, D. Harlow en J. Preskill.
Entropie en oppervlakte
Stel je een ruimte voor die op quantumniveau is opgebroken in allerlei minuscule ‘bits’, die allemaal met elkaar verstrengeld zijn. Meetkundige begrippen als lengte en oppervlakte betekenen op deze schaal niets meer. Hoe komt de ruimte op macroscopische schaal tevoorschijn?
In 2010 had de Canadese natuurkundige Mark van Raamsdonk hierover een belangrijk inzicht. Zijn hypothese is dat de ruimte verbonden is, juist doordat bits op quantumniveau verstrengeld zijn. Wij ervaren ruimte als een continu geheel: je kunt door de ruimte lopen, of zweven, zonder plekken tegen te komen waar ‘geen ruimte is’. Het idee van Van Raamsdonk is dat de verstrengeling de lijm is die de quantumbouwstenen van de ruimte bij elkaar houdt. Deze lijm zorgt er uiteindelijk voor dat lege ruimte op macroscopische schaal verbonden is.
Van Raamsdonks hypothese kan ook meer kwantitatief beschreven worden. Zijn idee is gebaseerd op een eenvoudige formule, oorspronkelijk afkomstig uit het werk van Bekenstein en Hawking aan zwarte gaten, maar in de context van quantuminformatie bestudeerd door de Japanse natuurkundigen Shinsei Ryu en Tadashi Takayanagi. De formule zegt het volgende: als we een stuk ruimte in twee gebieden opdelen, is de hoeveelheid verstrengeling tussen deze gebieden gelijk aan
S = A / (4 G ħ)
In deze formule staat S voor de zogeheten verstrengelingsentropie – een maat voor de hoeveelheid informatie die de twee gebieden met elkaar delen. A is de grootte van het denkbeeldige oppervlak dat de twee gebieden scheidt. Verder zijn G en ħ twee natuurconstantes: de constante van Newton, G, bepaalt hoe sterk de zwaartekracht is, terwijl de constante van Planck, ħ, aangeeft op welke schaal quantumeffecten een rol spelen.
We kunnen de vorm van deze formule gemakkelijk begrijpen. De twee gebieden, laten we ze gemakshalve 1 en 2 noemen, delen niet-lokale quantuminformatie, omdat er in gebied 1 quantumbits zijn die verstrengeld zijn met quantumbits in gebied 2. Als we verstrengeling volgens Van Raamsdonks hypothese zien als de eigenschap die ruimte verbindt, ligt het voor de hand dat de meeste verstrengeling plaatsvindt rond de grens tussen 1 en 2. De hoeveelheid informatie die de twee gebieden delen, S, is daarom proportioneel met de oppervlakte van die grens, A. De factor 4Għ bepaalt de precieze verhouding tussen de twee grootheden.
Dit verschijnsel, dat een hoeveelheid informatie gerelateerd is aan een oppervlakte, blijkt een essentiële eigenschap van Einsteins zwaartekrachtstheorie. In 1995 toonde Ted Jacobson aan dat deze relatie zelfs noodzakelijk is om de zwaartekrachtswetten van Einstein te kunnen afleiden. Omgekeerd zou een correctie op deze relatie dus noodzakelijkerwijs moeten leiden tot een aanpassing van de zwaartekrachtswetten. Waar zou een dergelijke correctie vandaan kunnen komen?
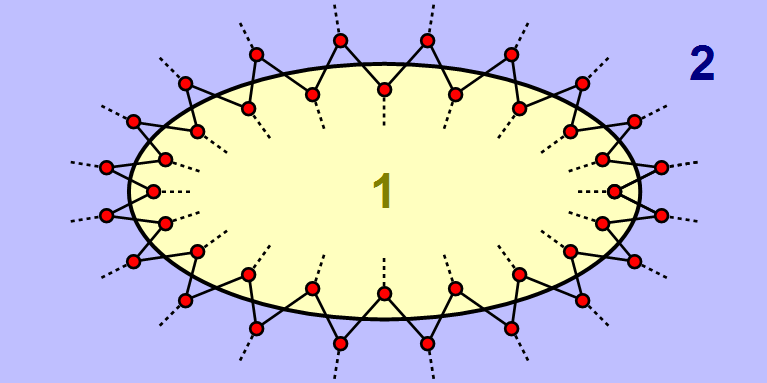
Afbeelding 4. Verstrengeling, informatie en oppervlak.Als verstrengeling de ruimte verbindt, zal de verstrengeling tussen bits in gebied 1 en bits in gebied 2 met name plaatsvinden rond het oppervlak dat de gebieden scheidt. Het is dus niet verrassend dat de informatie die de gebieden delen ook proportioneel is met de grootte van dat oppervlak.
Positief en negatief gekromde ruimte
De meetkundige eigenschappen van de ruimte om ons heen hebben een grote invloed op de aard van de zwaartekracht. Ons heelal is op grote schaal geen vlak toneel: de ruimte is gekromd. Volgens de theorie kan een dergelijke kromming twee vormen hebben. Het heelal kan ‘positief’ gekromd zijn, zoals het oppervlak van een bol, of ‘negatief’, zoals het zadel van een paard. Er is een direct verband tussen deze kromming en het raadsel van de afstotende donkere energie. Een negatieve kromming van het heelal zou leiden tot een grootschalige extra aantrekkingskracht. In ons heelal is echter het omgekeerde aan de hand: de donkere energie leidt tot een positieve kromming, die op haar beurt zorgt voor de afstotende kracht die wordt waargenomen in de versnellende uitdijing van de ruimte.

Afbeelding 5. Positieve en negatieve kromming.Links een positief gekromd oppervlak, rechts een oppervlak met negatieve kromming. Onze vierdimensionale ruimtetijd kan op soortgelijke wijze positief en negatief gekromd zijn.
Om hun relatie tussen informatie en oppervlakte te kunnen aantonen, moesten Ryu en Takayanagi aannemen dat de ruimte negatief gekromd is. Zoals gezegd leven wij echter niet in zo’n negatief gekromd heelal, maar in een positief gekromd ruimte – ook wel een De Sitterheelal genoemd. Het theoretisch beter begrepen negatief gekromde geval – dat niet geheel verrassend een Anti-de Sitterheelal wordt genoemd – is op grote schaal, als de kromming van het heelal een rol gaat spelen, slechts een benadering van de werkelijkheid.
Het grootste verschil tussen een Anti-de Sitterheelal en een De Sitterheelal is dat de laatste ruimte energie bevat. Een Anti-de Sitterheelal kan gezien worden als een ‘lege’ vacuumtoestand, terwijl een De Sitterheelal een hoog-energetische toestand is. De extra energie in een De Sitterheelal is de donkere energie die voor de uitdijing van het heelal zorgt.
De vragen die Verlinde zichzelf stelde zijn: welke gevolgen hebben de extra energie en de extra kromming voor de verdeling van de informatie in de ruimtetijd, en wat betekenen die gevolgen voor de zwaartekracht? Het was hem al snel duidelijk dat de relatie van Ryu en Takayanagi, die informatie en oppervlak relateert, nog eens goed onder de loep genomen moest worden.
Donkere energie: een volumebijdrage aan de entropie
Geldt de relatie tussen informatie en oppervlakte ook in een De Sitterheelal? Volgens Verlinde is het antwoord ‘ja’, maar is er naast de oppervlaktecomponent nóg een bijdrage aan de entropie. Deze extra informatie, die geassocieerd is met de donkere energie, is in Verlindes model verspreid over de hele ruimte. Daarom hangt deze bijdrage aan de hoeveelheid informatie af van het volume van een stuk ruimte, en niet van de oppervlakte ervan.
Ook deze relatie kan weer in een formule worden weergegeven. De extra volumebijdrage aan de entropie binnen een bolvormig oppervlak is gelijk aan
S = A R / (4 G L ħ)
Hierin is L de kosmologische schaal: de afstand tot de rand van het zichtbare universum. Verder is A = 4 π R2 de oppervlakte van een bolvormig stuk ruimte met straal R, en zijn G en ħ weer de constantes van Newton en Planck.
Om in te zien dat het hier daadwerkelijk gaat om een bijdrage die proportioneel is met het volume moeten we ons realiseren dat het volume van een bol gegeven wordt door V = 4/3 π R3. Met wat eenvoudige algebra valt bovenstaande formule dan ook te schrijven als
S = V / V0
waarin V0 staat voor de combinatie 4 G ħ L / 3. We kunnen V0 zien als het volume dat één bit aan informatie in de donkere energie inneemt: het totale volume gedeeld door V0 is volgens de formule immers gelijk aan de hoeveelheid informatie in de donkere energie, S. Een belangrijke opmerking is dat de volumebijdrage (2) aan de entropie meestal veel kleiner zal zijn dan de oppervlaktebijdrage (1). De twee uitdrukkingen verschillen een factor R / L van elkaar; als we voor R bijvoorbeeldde straal van ons melkwegstelsel nemen, is deze factor grofweg gelijk aan 0,00001.
De volgende vraag is dan ook: als de volumebijdrage aan de entropie zelfs op de schaal van hele sterrenstelsels zo klein is, kan die dan toch een waarneembaar effect hebben? Verlindes theorie beantwoordt deze vraag verrassend genoeg bevestigend. De volumebijdrage zorgt ervoor dat juist op de schaal van sterrenstelsels de zwaartekrachtswetten van Newton en Einstein niet meer exact gelden.

Afbeelding 6. Informatie in een De Sitterheelal.Doordat een De Sitterheelal is gevuld met donkere energie, kan niet alle informatie op de rand afgebeeld worden. Juist de informatie in de donkere energie zelf, hier schematisch weergegeven met de blauwe blokjes, is proportioneel met het volume.
Het ontstaan van gewone materie
Het universum bestaat natuurlijk niet alleen uit donkere energie. Het bevat ook de gewone materie waaruit alles is opgebouwd wat we om ons heen zien. Pas als we gewone materie toevoegen aan een De Sitterheelal wordt duidelijk dat de bestaande zwaartekrachtswetten moeten worden aangepast.
Gewone materie kan volgens Verlinde ontstaan doordat donkere energie uit het heelal wordt weggenomen en ergens wordt gelokaliseerd. De creatie van een massa, zoals de zon, laat echter een blijvend ‘litteken’ achter in een De Sitterheelal. Het heelal herinnert zich als het ware dat er een massa gecreëerd is. Ten eerste kromt daardoor de ruimte, waardoor andere massa’s, zoals de aarde, tot de materie worden aangetrokken. Die kromming beschreef Einstein al in zijn algemene relativiteitstheorie.
Er is echter nog een tweede effect. Het ontstaan van een massa beïnvloedt ook de informatieverdeling die hoort bij de donkere energie. Een deel van de informatie is nu geassocieerd met de materie, waardoor het andere deel zich moet herschikken in de ruimte. Massa verplaatst dus informatie. Een actie leidt echter altijd tot een reactie: de informatie ‘duwt’ ook terug. Op de schaal van sterrenstelsels en clusters van sterrenstelsels wordt dusdanig veel materie weggenomen dat dit effect, ondanks de relatief kleine bijdrage van de donkere energie aan de totale informatie, toch significant is. De resulterende extra kracht wordt dan ook op deze schaal al waargenomen: het is precies de kracht die wordt toegeschreven aan de donkere materie!
Ook deze uitspraak kan weer kwantitatief worden gemaakt. Op plekken waar informatie is weggehaald, ontstaat lege ruimte, terwijl daarbuiten de ruimte nog steeds gevuld is met informatie en energie. Vooral rond materie bevindt zich dus de meeste lege ruimte. Dit betekent dat er rond een massa op een bepaalde afstand een overgang is van lege naar gevulde ruimte.
Verlinde berekent deze overgangsafstand als volgt. De hoeveelheid informatie die geassocieerd is met materie, en die wordt weggehaald uit de donkere energie, is in zijn model van emergente zwaartekracht gelijk aan
SM = 2 π M R / ħ
SM is hierin de hoeveelheid ‘weggenomen’ informatie, M de massa van de materie, en R de straal van het gebied waarbinnen die materie zich bevindt. De overgang van lege naar gevulde ruimte treedt precies op wanneer de hoeveelheid informatie die geassocieerd is met de donkere energie, vergelijking (2), begint te domineren over de hoeveel informatie die door de materie is weggenomen, vergelijking (3). De zwaartekrachtseffecten die worden toegekend aan donkere materie beginnen dus op te treden als
A / (4 G ħ) > 2 π M L / ħ
Deze formule is zo geschreven dat aan de linkerkant de bekende combinatie staat uit de formule van Ryu en Takayanagi, formule (1). De oppervlakte A die uit deze formule berekend kan worden, geeft de grens aan van het gebied waarbuiten ‘donkere materie’ in bijvoorbeeld een sterrenstelsel een rol gaat spelen. Deze grens blijkt goed overeen te komen met wat daadwerkelijk in sterrenstelsels wordt waargenomen.
Merk op dat in de bovenstaande formule de kosmologische schaal L voorkomt. Die factor is afkomstig uit de eerdere formule (2), voor de hoeveelheid informatie die zit in donkere energie. Verrassenderwijs wordt de extra zwaartekracht, die we waarnemen op de schaal van individuele sterrenstelsels, dus bepaald door natuurkunde op de schaal van de hele kosmos!

Afbeelding 7. Materie in een De Sitterheelal.Materie, zoals een sterrenstelsel, wordt gevormd uit de informatie die geassocieerd is met de donkere energie. Hierdoor ontstaat een gebied aan ‘lege’ ruimte, die op een bepaalde afstand overgaat ruimte gevuld met informatie. Rond sterrenstelsels komt deze afstand goed overeen met de waargenomen afstand waarop ‘donkere materie’ een rol gaat spelen.
Een formule voor donkere materie
De uitleg hierboven dient voor Verlinde als motivatie voor het afleiden van zijn belangrijkste resultaat: een algemene relatie tussen de daadwerkelijke hoeveelheid gewone materie en de schijnbare hoeveelheid donkere materie. Volgens hem bestaat die donkere materie zoals gezegd niet, maar we kunnen de eraan toegeschreven effecten beschrijven aan de hand van een effectieve massa – de massa die de donkere materie zou hebben gehad als die wél de verklaring was geweest voor de extra zwaartekracht. Verlinde leidt voor deze effectieve massa, MD, de volgende relatie af:
2 π L / ħ (MD)2 = MB / 3 A / (4 G ħ)
MB is hierin de hoeveelheid gewone (‘baryonische’) materie; alle andere symbolen zijn zoals hierboven al beschreven. Twee dingen vallen op aan deze formule. Ten eerste bevat die weer de kosmologische schaal L: ook hier zien we weer dat de grootte van het effect van donkere materie wordt bepaald door natuurkunde op de schaal van de hele kosmos. Verder valt het op dat er überhaupt een verband is tussen de hoeveelheid gewone en de schijnbare hoeveelheid donkere materie. Dit is een manifestatie van wat hierboven is uitgelegd: ‘donkere materie’ is een reactiekracht die ontstaat als informatie wordt weggenomen om gewone materie te vormen. Het is dus niet verbazend dat er een verband tussen de twee bestaat. Verlindes formule maakt dit verband heel precies.
Conclusie
Emergentie, het ontstaan van zwaartekracht op grote schaal uit informatieverdeling op kleine schaal, lost wellicht drie problemen tegelijkertijd op. Ten eerste bestaat de zwaartekracht zoals wij die kennen op de allerkleinste schaal niet, en is een begrip van de zwaartekrachtswetten op quantumschaal dus overbodig. Ten tweede bestaat de ruimte op quantumniveau uit informatiebits die met elkaar verstrengeld zijn. Als de microtoestand van alle bits een hoge energie heeft, is de ruimte op grote schaal gezien een De Sitterheelal. Dit verklaart de oorsprong van donkere energie. Ten derde verplaatst het creëren van een massa in een De Sitterheelal de informatie die geassocieerd is met de donkere energie. Deze verplaatsing van informatie heeft zijn weerslag op massa’s die zich bijvoorbeeld aan de rand van een sterrenstelsel bevinden. Deze reactiekracht komt overeen met de effecten die worden toegeschreven aan de mysterieuze donkere materie.
Het oplossen van drie problemen in één klap is een prachtig vooruitzicht, maar kunnen Verlindes ideeën ook getest worden? Dat kan zeker: we hebben gezien dat zijn theorie niet alleen kwalitatieve beschrijvingen geeft, maar ook kwantitatieve formules oplevert die met waarnemingen geverifieerd kunnen worden. Omgekeerd is een falsificatie natuurlijk ook mogelijk: zodra één van de vele huidige zoektochten een daadwerkelijk materiedeeltje vindt als verklaring voor de donkere materie, blijkt Verlindes theorie natuurlijk onjuist.
Ook als Verlindes theorie juist blijkt, is er nog veel werk aan de winkel. Een grote open vraag is bijvoorbeeld hoe de dynamica van het heelal haar intrede doet in zijn formulering: kan dit idee ook de geschiedenis van de kosmos, en het in de loop van de tijd bewegen van materie en ‘donkere materie’, precies beschrijven? Kunnen hiermee zelfs eigenschappen van de kosmische achtergrondstraling, het licht dat we nu nog steeds opvangen uit het allervroegste heelal, verklaard worden? Daarnaast wordt in sommige waarnemingen, zoals bijvoorbeeld aan de zogeheten Bulletcluster, niet alleen de verhouding tussen gewone en ‘donkere’ materie gemeten, maar ook de manier waarop deze twee over de ruimte verdeeld lijken te zijn. Die verdeling blijkt niet altijd mooi symmetrisch, en het is dus een mooie uitdaging voor Verlindes model om ook dergelijke waarnemingen te verklaren.
Hoe het ook zij, de ideeën van Erik Verlinde klinken zonder meer aantrekkelijk, en bieden een interessante alternatieve zienswijze op decennia-oude fundamentele problemen rond de zwaartekracht. Hopelijk draagt zijn theorie eraan bij dat we deze alledaagse kracht, die mensen al miljoenen jaren ervaren, op niet al te lange termijn ook daadwerkelijk zullen begrijpen.