Als je de omtrek C van een cirkel met straal r wilt bepalen vermenigvuldig je simpelweg de straal van de cirkel met 2π. Dit is correct, maar hoe kom je eigenlijk aan zo’n formule? Zo’n formule leid je af door een integraal op te stellen die van hele kleine stukjes van de cirkel de lengte bepaalt en die allemaal bij elkaar optelt. Zo vind je C=2πr. Wil je nu hetzelfde doen voor een ellips, dan kom je al snel een integraal tegen die je niet in een mooie vorm kunt opschrijven. Deze integraal wordt een elliptische integraal genoemd. Stel nu dat je alleen maar in een gedeelte van de omtrek van een ellips geïntereseerd bent; dus tot een hoek θ. De omtrek C is dan een functie van θ. Het blijkt nu dat dit, als je gaat kijken naar de inverse, dus θ als een functie van C, veel mooiere functies oplevert. De hoek θ wordt dan gegeven in termen van een zogeheten Jacobi elliptische functie. Deze functies zijn erg speciaal, want ze hebben een zogenaamde dubbele periodiciteit.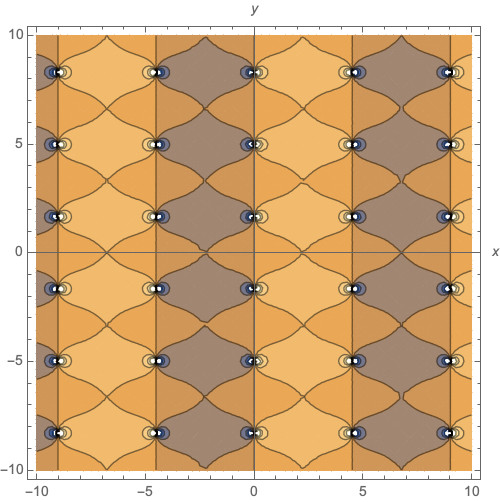
Afbeelding 1. Een Jacobi elliptische functie.De Jacobi elliptische functie als functie vanhet complexe getal z=x+iy, waarbij x horizontaal is en y verticaal. De kleuren geven de hoogte van de Jacobi elliptische functie aan.
Om uit te leggen wat dubbel periodiek is moet ik eerst iets vertellen over complexe getallen. Deze getallen zijn bijna hetzelfde als de reële getallen, maar met de extra eigenschap dat we ook de wortel van negatieve getallen kunnen nemen. Om dat te kunnen doen defineren we een nieuw getal i als de wortel van -1, dus i2 = -1. Een complex getal z bestaat uit twee delen: een reeël deel x en een imaginair deel y. We schrijven z dan als z=x+iy, waarbij x en y gewone getallen zijn. Natuurlijk valt er nog veel meer te zeggen over complexe getallen. Als je daar meer over wilt lezen, kijk dan hier.
De Jacobi elliptische functie hangt af van een reële variabele x – voorheen was dat de lengte C. Zoals je makkelijk kunt nagaan is deze functie periodiek in x, want als je bij C de lengte van de hele ellips optelt blijft de hoek θ hetzelfde. Als je nu niet een reeële variabele x maar een complexe variabele z=x+iy neemt, dan blijkt dat de Jacobi elliptische functie óók periodiek is in y; dus dubbel periodiek! In afbeelding 1 kun je goed zien dat deze functie inderdaad periodiek is in zowel de x- als y-richting.
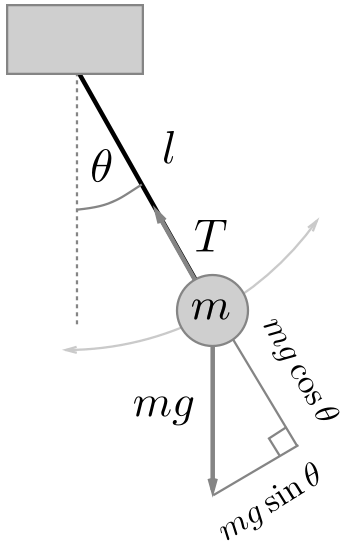
Afbeelding 2. Slinger.In deze afbeelding kun je zien welke krachten er op een slinger werken. Door de hoekversnelling α en de normale versnelling a te relateren als α=al en de wetten van Newton te gebruiken, kun je de onderstaande vergelijking afleiden. Afbeelding uit dit artikel van Alexei Gilchrist.
Nu zul je je vast afvragen, en terecht, wat dit met natuurkunde te maken heeft. Er is een heel eenvoudig voorbeeld waar deze dubbel periodieke functies voorkomen, namelijk de slinger. Door middel van een krachtenbalans, zie afbeelding 2, kun je als je wat mechanica-achtergrondkennis hebt afleiden dat voor een slinger de volgende relatie geldt,
m·α= -mg·sin(θ)/l,
waarbij θ een functie van de tijd t is en α de hoekversnelling – dus de tweede afgeleide van θ naar de tijd t. De oplossing als functie van tijd t, θ(t), is een erg ingewikkelde functie die geen mooie vorm heeft. Één ding weten we wil zeker: θ(t) is periodiek in de tijd met een bepaalde periode T, dus θ(t+T)=θ(t).
De vraag die we nu willen beantwoorden is of θ(t) ook dubbel periodiek is. Om daar achter te komen, gebruiken we dezelfde methode als hierboven en kijken we naar complexe tijd τ = t + it1. Stel nu dat je naar een fictieve puur complexe tijd wil kijken, dus τ = it1. De tweede afgeleide van θ(τ) naar τ kun je nu schrijven als minus de tweede afgeleide van theta naar t1. Voor de wiskundeliefhebbers: dit kun je laten zien door de kettingregel te gebruiken en dat i2 = -1. Het feit dat de hoekversnelling α nu van teken is veranderd, betekent dat de zwaartekracht in de tegenovergestelde richting wijst en de slinger dus oscilleert rondom de rechtopstaande positie. Je ziet daaruit dat de slinger in dit geval in tijd t1 nog altijd periodiek is, en dus is de exacte oplossing voor de uitwijking θ als functie van complexe tijd τ dubbel periodiek. Het is zelfs zo dat de je de exacte oplossing kunt schrijven in termen van de Jacobi elliptische functie die we ook tegenkwamen bij het bepalen van de omtrek van een ellips. Deze functie noemt men ook wel de sinus amplitudinis en dit is de functie die is weergegeven in afbeelding 1.
In het volgende artikel in dit tweeluik zullen we gaan kijken naar speciale typen meetkundige vormen, de elliptische krommen, en zullen we de link leggen met dubbel periodieke functies. Bovendien zullen we ook zien wat voor een rol deze relatie in natuurkunde speelt.
De theorie die ik hier heb geprobeerd uit te leggen is niet erg gemakkelijk om direct te begrijpen, maar als er vragen zijn kunnen die natuurlijk altijd op het forum gesteld worden!