Afbeelding 1. De Baron von Münchhausen trekt zichzelf uit het moeras.Gravure door Gustave Doré (1862).
Quantummechanica: van klein naar groot
Van oorsprong is de quantummechanica een theorie die – zeer succesvol – het gedrag van de kleinste deeltjes beschrijft: elektronen, fotonen, atomen en moleculen. Maar wat gebeurt er op veel grotere schaal? Om daarover na te denken gebruiken natuurkundigen vaak gedachte-experimenten, met als beroemdste voorbeeld waarschijnlijk Schrödingers kat. Grofweg gaat dat experiment als volgt: een kat wordt opgesloten in een stalen doos, samen met een buisje waarin een klein beetje radioactief materiaal zit, een geigerteller, een hamertje en een flesje blauwzuur. Als één van de atomen in het buisje vervalt, gaat de geigerteller af, waardoor het hamertje het flesje blauwzuur kapot slaat en de kat sterft.
Radioactiviteit is een subatomaire aangelegenheid en valt daarmee binnen het domein van de quantummechanica: er is daarom een bepaalde kans dat een atoom al dan niet vervalt. De zogeheten ‘toestand’ van het atoom is daarom een superpositie van ‘vervallen’ + ‘niet-vervallen’. De vraag is nu: is de toestand van het gehele systeem daarom ook een combinatie van de toestanden ‘kat levend’ + ‘kat dood’, waarin dus niet slechts één van die twee uitkomsten gerealiseerd is? Kunnen we de wetten van de quantummechanica extrapoleren naar katten, mensen, en zwarte gaten? Met andere woorden: is de quantummechanica universeel?
Een gedachte-experiment
Dit is de vraag die ook ter discussie staat in het nieuwe gedachte-experiment van de theoretisch natuurkundigen Renato Renner en Daniela Frauchiger. Voor we dit experiment onder de loep nemen kijken we eerst naar de implicaties voor een openstaand probleem: de interpretatie van de quantummechanica. De verschillen in interpretatie van die theorie gaan meestal over wat er gebeurt bij een meting van de golffunctie, de abstracte wiskundige manier waarop we een toestand van een deeltje beschrijven. In de bekendste, zogeheten Kopenhagen-interpretatie zorgt een meting van bijvoorbeeld de positie van een deeltje ervoor dat de golffunctie (die in dit geval de waarschijnlijkheid beschrijft dat het deeltje zich op een bepaalde positie bevindt) ‘ineenstort’ en het deeltje zich ineens op een vaste, bepaalde positie bevindt; we kunnen in die interpretatie dus niet spreken over de exacte positie van een deeltje, totdat die positie gemeten is. Een andere interpretatie, die van de vele-werelden, stelt dat die ineenstorting nooit plaatsvindt: alle mogelijke uitkomsten van een meting gebeuren, maar allemaal in een andere “wereld”.
Renner en Frauchiger doen in hun gedachte-experiment drie heel redelijk klinkende aannames en komen uiteindelijk tot een tegenstelling. De conclusie is daarom dat één van die volgende drie aannames fout moet zijn:
- (A) Tegengestelde feiten kunnen niet tegelijkertijd waar zijn: het kan niet zo zijn dat A = B en A ≠ B.
- (C) Quantummechanica is consistent: de voorspellingen die gedaan worden door verschillende waarnemers zijn niet tegenstrijdig.
- (Q) Quantummechanica is universeel: alles in het heelal, van kleine deeltjes tot grote laboratoria, volgt de wetten van de quantummechanica.
Het gedachte-experiment laat daarmee zien dat elke interpretatie van de quantummechanica (tenminste) één van deze aannames moet opgeven. Zo geeft de vele-werelden interpretatie bijvoorbeeld aanname (A) op – twee waarnemers in verschillende “werelden” kunnen verschillende waarnemingen doen – en schendt de Kopenhagen interpretatie zoals we zullen zien aanname (C).
Tossen en spinnen
Genoeg over de implicaties: tijd om het gedachte-experiment zelf onder de loep te nemen. Daarvoor hebben we vier mensen nodig: Alice en haar vriendin, en Bob en zijn vriend. De vriendin van Alice (A’) doet een meting aan een quantummechanisch systeem in een lab, en Alice zelf (A) zit daarbuiten, terwijl ze zowel het lab als haar vriendin observeert. Evenzo zit Bobs vriend (B’) in een lab, en Bob (B) daarbuiten, terwijl hij zijn vriend en het lab als één systeem bestudeert. In het eerste lab gooit de vriendin van Alice steeds een muntje op, waarmee zodanig geknoeid is dat ze een derde van de tijd kop gooit, en twee derde munt. Afhankelijk van de uitkomst zorgt ze er vervolgens voor dat een deeltje in één van twee mogelijke toestanden gebracht wordt: gooit ze kop, dan geeft ze het deeltje spin omlaag, een heel precieze draaitoestand dus, en als ze munt gooit, dan brengt ze het deeltje in een superpositie van twee draaitoestanden: spin omhoog en spin omlaag. Daarna stuurt ze haar deeltje naar Bobs vriend, die de spin van het deeltje meet. Afhankelijk van de uitkomst kan Bobs vriend nu iets zeggen over wat Alice’s vriendin zag toen ze een muntje opgooide – als hij bijvoorbeeld spin omhoog meet, dan weet hij zeker dat ze munt gooide.
Nu komt het ingewikkelde stuk van het experiment. Alice meet de gecombineerde toestand van haar vriendin en het lab, waarbij ze alles ziet als één quantummechanisch systeem. Hierin schuilt aanname (Q): het idee dat quantummechanica universeel is, en alles in het heelal – dus ook hele laboratoria, en de wetenschappers daarin – haar wetten volgt. Het punt is nu dat Alice zogezegd een meting ‘langs een andere as’ doet, waardoor die meting het lab en haar vriendin in een superpositie brengt van de toestanden ‘Alice’ vriendin heeft munt gegooid’ en ‘Alice’ vriendin heeft kop gegooid’. Alice’ meetapparaatje geeft een simpel ‘ja’ of ‘nee’. (De precieze betekenis van ‘ja’ en ‘nee’ is ingewikkeld en zullen we hier niet toelichten – het gaat er vooral om dat er in het experiment dat de onderzoekers voorstellen twee opties zijn.) De uitkomst die Alice meet zorgt er vervolgens voor dat ze ook iets kan zeggen over de meting die Bobs vriend heeft gedaan. Stel dat ze bijvoorbeeld ‘ja’ meet, dan kan ze beredeneren (door gebruik te maken van de wetten van het experiment en van de quantummechanica) dat Bobs vriend spin omhoog heeft gemeten, en dus dat Alice’ vriendin munt heeft gegooid.
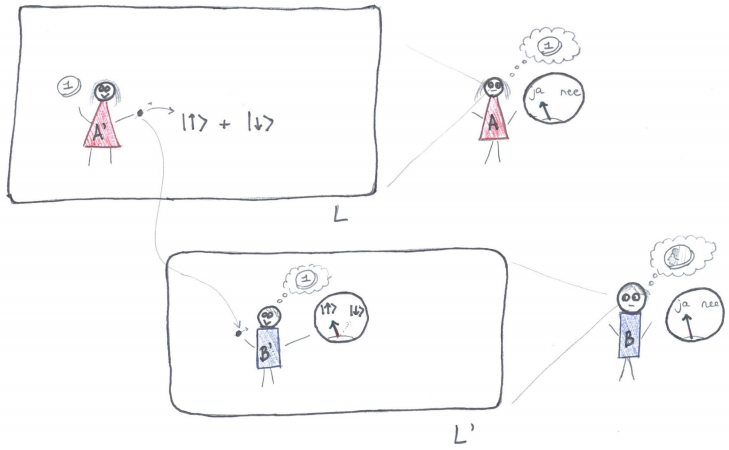
Afbeelding 2. Het experiment.Een schets van het experiment dat Alice, Bob en hun twee vrienden uitvoeren.
Duizelt het al? Het belangrijkste van dit deel van het experiment is dat hier de tweede aanname in schuilt: die van consistentie (C). Alice gebruikt namelijk in haar eigen redenering ook de argumentatie van Bobs vriend. Ze neemt daarbij aan dat de voorspellingen die andere waarnemers doen op basis van quantummechanica niet tegenstrijdig zijn met haar eigen voorspellingen.
Tot slot hebben we nog Bob. Net als Alice doet hij een ingewikkelde meting aan zijn vriend en diens laboratorium, waardoor hij ze in een quantumsuperpositie plaatst. Ook voor Bob is de uitkomst op zijn meetapparaatje ‘ja’ of ‘nee’. Het experiment is zo ontworpen dat als Bob ‘ja’ krijgt, hij dan concludeert dat Alice’ vriendin kop gegooid moet hebben.
Wat is nu de crux van het experiment? Alice en Bob kunnen hun uitkomsten vergelijken. Als Alice ‘ja’ krijgt, concludeert ze dat haar vriendin munt heeft gegooid. Als Bob ‘ja’ krijgt, trekt hij de conclusie dat kop werd gegooid. De eerste aanname, (A), komt hier naar voren: Alice’ vriendin kan niet tegelijkertijd kop en munt hebben gegooid. Er is dus niets aan de hand zolang Alice en Bob tegengestelde antwoorden krijgen. Door echter precies uit te rekenen met welke waarschijnlijkheid Alice en Bob hun uitkomsten meten, blijkt dat in 1/12 van de gevallen ze allebei ‘ja’ meten, en het dus oneens zijn over wat Alice’ vriendin gegooid heeft.
Something’s gotta give…
Dit brengt ons bij de conclusie die we eerder al noemden: het kan niet zo zijn dat een quantummechanische theorie aan zowel (A), (C), als (Q) voldoet. Volgen we de Kopenhagen-interpretatie, dan volgt dat het grootschalige systeem niet het kleinschalige quantumsysteem getrouw kan modelleren – geen quantum-Baronnen, dus. Welke aanname we echter moeten opgeven wordt niet duidelijk uit het experiment. Het is daarmee vooral een manier om de bestaande verschillende interpretaties te classificeren – en mocht er een nieuwe interpretatie ontwikkeld worden, dan hebben we direct een test om die aan te onderwerpen.
Vooralsnog blijft het overigens wel bij een gedachte-experiment. Als we dit experiment daadwerkelijk willen uitvoeren, dan treedt er namelijk een gevoelige complicatie op: de meting van Alice brengt immers alles – inclusief het brein van haar vriendin – in een superpositie van toestanden. Dit betekent ook dat Alice de tijdsevolutie zal moeten terugdraaien, zodat het geheugen van haar vriendin gewist wordt. Met mensen is dit vooralsnog niet mogelijk – de ethische kant nog daargelaten. Wellicht kan in de toekomst echter wel een soortgelijk experiment gedaan worden met quantumcomputers, om erachter te komen op welk punt in de theoretische redenering het mis gaat en welke aanname dus moet worden opgegeven. Wie weet is er dus nog hoop voor onze quantum-Baron von Münchhausen, en blijkt de quantummechanica zichzelf wél consistent te kunnen beschrijven.
