In de natuurkunde is het vaak nuttig om de toestand van een systeem te beschrijven als een punt in een meerdimensionale configuratieruimte. Wanneer twee auto’s bijvoorbeeld over een weg van 1 km rijden (zie afbeelding 1), kunnen we de posities van de twee auto’s aangeven door middel van twee stippen op een lijn. We kunnen de twee posities echter ook aangeven door middel van één stip in een vierkant. Op een soortgelijke manier kunnen we de posities van drie auto’s aangeven als een punt in een driedimensionale kubus, en die van vier auto’s als een punt in een vierdimensionale “hyperkubus”. Zo’n hyperkubus (net als de nog hogerdimensionale varianten daarop) valt in onze driedimensionale ruimte niet te tekenen, maar wiskundig kunnen we zo’n vier- of hogerdimensionale configuratieruimte zonder veel problemen hanteren.
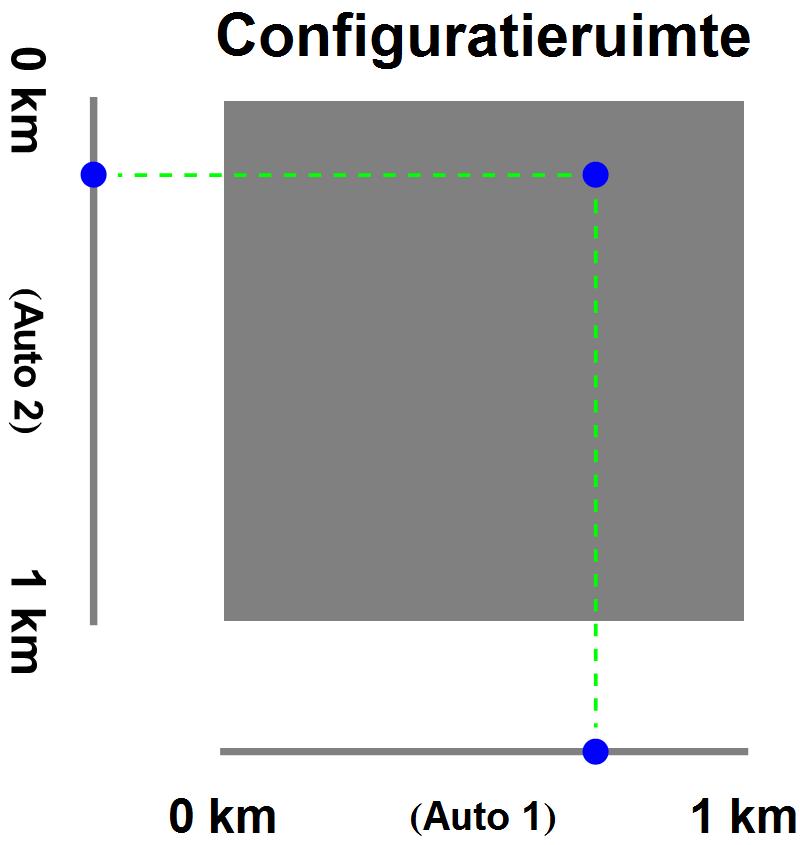
Afbeelding 1. ConfiguratieruimteEen eenvoudig voorbeeld van een configuratieruimte. Twee auto’s rijden over een weg van 1 km lengte. We kunnen de auto’s elk aangeven als een afzonderlijke stip op een lijn die de weg voorstelt, maar we kunnen de gecombineerde posities ook aangeven door middel van één stip in een tweedimensionaal vierkant.
Behalve de posities van de auto’s kunnen we ook hun snelheden, versnellingen, enzovoort, als extra dimensies in een dergelijke configuratieruimte opnemen. Voor veel natuurkundige systemen blijkt het voldoende te zijn om alleen de posities en snelheden (of preciezer: impulsen) van de diverse componenten in een configuratieruimte op te nemen. Andere eigenschappen, zoals de versnelling, liggen voor dergelijke systemen namelijk vast zodra de posities en impulsen bekend zijn. Een configuratieruimte waarin de diverse dimensies paarsgewijs overeenkomen met dergelijke positie-impulsparen heet een faseruimte.
In de klassieke mechanica is de faseruimte een nuttig hulpmiddel om de bewegingswetten van mechanische systemen te begrijpen. Een belangrijke rol daarbij wordt gespeeld door de wiskundige stelling van Liouville. Deze stelling zegt dat systemen waarvan we de beginposities en -impulsen kiezen in een gebied in de faseruimte met een bepaalde oppervlakte (of hogerdimensionaal volume), zich altijd zullen blijven bevinden in een gebied met precies diezelfde oppervlakte – zie afbeelding 2 voor een voorbeeld.

Afbeelding 2. De stelling van LiouvilleAls de posities en impulsen van een systeem op een bepaald moment binnen een gebied met een bepaald volume vallen, vallen die posities en impulsen op elk later moment binnen een gebied met hetzelfde volume. (De vorm van het gebied kan zoals we zien in de loop van de tijd wel veranderen.) Klassiek gezien kunnen binnen zo’n gebied oneindig veel verschillende systemen vallen; quantummechanisch is dit aantal eindig. Het aantal toestanden dat binnen een bepaald nauwkeurigheidsgebied in de faseruimte valt, is gelijk aan de oppervlakte van dat gebied (of algemener: het hogerdimensionale volume) ten opzichte van de oppervlakte van een “Planckcel”. De Planckcellen zijn hier aangegeven door de grijze vierkantjes.
In de quantummechanica speelt de faseruimte ook een belangrijke rol. Voor quantummechanische systemen kunnen we nooit tegelijk de posities en impulsen met willekeurige precisie meten – het zogenaamde onzekerheidsprincipe van Heisenberg. We kunnen de posities en impulsen van een quantummechanisch systeem daardoor niet weergeven als een punt in de faseruimte, maar hooguit als een gebied dat de onzekerheid in de posities en impulsen aangeeft. Het oppervlak (of volume) van een dergelijke “cel” wordt bepaald door een fundamentele natuurconstante: de constante van Planck.
Dit houdt direct verband met een belangrijk feit uit de quantummechanica: waar we in de klassieke mechanica, door de beginvoorwaarden iets te veranderen, een systeem in een oneindig aantal verschillende toestanden kunnen brengen, is de verzameling mogelijke toestanden in de quantummechanica discreet – de toestanden zijn gequantiseerd. Niels Bohr en Arnold Sommerfeld ontdekten hoe deze quantisatie preciezer gemaakt kan worden: als we tellen hoeveel van bovenstaande “Planckcellen” een gebied in de faseruimte bevat, weten we ruwweg hoeveel verschillende mogelijke quantumtoestanden er binnen de bijbehorende grenzen aan de posities en impulsen vallen. De stelling van Liouville wordt hiermee een logisch resultaat: die stelling zegt niets anders dan dat het aantal toestanden dat we beschrijven in de loop van de tijd niet verandert.
Het tellen van toestanden in de faseruimte speelt een belangrijke rol in het bepalen van de entropie van een systeem – een grootheid die iets zegt over de hoeveelheid informatie die we over een systeem bezitten. Over de precieze relatie tussen faseruimte en entropie, en over alle andere hierboven kort beschreven onderwerpen, wordt veel meer verteld in de rest van dit dossier. Rechts bovenaan deze pagina vind je een overzicht van de artikelen in dit dossier. Je kunt ook direct beginnen met het lezen van het eerste artikel, waarin het begrip entropie nader wordt uitgelegd.
Afbeeldingsverantwoording: de afbeelding uit het blokkenschema is afkomstig van Telecom Italia-site.