De verbondenheid van water
Heb je je wel eens afgevraagd waarom er geen lege ruimtes zijn in een bak met water? Dit lijkt wellicht vanzelfsprekend – we kunnen immers zwemmen in de zee zonder grote obstakels tegen te komen waar “geen water” is – maar als je je bedenkt waar water uit bestaat (moleculen met veel lege ruimte ertussen), dan is dit juist heel wonderlijk.
We weten dat “water” er op kleine schaal anders uitziet dan op grote schaal. Op kleine schaal bestaat water uit H2O-moleculen, die bij elkaar worden gehouden door waterstofbruggen. Deze waterstofbruggen zijn zo sterk dat op grote schaal water vloeibaar, of anders gezegd, “continu verbonden” is. Hiermee bedoelen we dat er in principe geen lege ruimtes aanwezig zijn in een bak met water – op een paar luchtbellen na dan.
Deze continue verbondenheid van water is een voorbeeld van emergentie. Emergentie is simpel gezegd het fenomeen dat op grote schaal er nieuwe eigenschappen optreden die op kleine schaal niet aanwezig zijn.
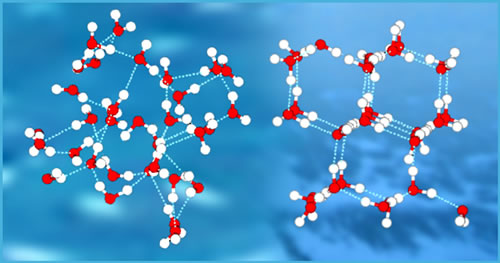
Afbeelding 1. Watermoleculen.
De waterstofbruggen tussen H2O-moleculen houden de moleculen bij elkaar. Deze sterke molecuulbinding zorgt er op grote schaal voor dat water vloeibaar is.
Bron: http://www2.lbl.gov/Science-Articles/Archive/sabl/2005/February/water-solid.html.
De verbondenheid van ruimte
Over ruimte kunnen we een soortgelijke vraag stellen: waarom is de ruimte om ons heen continu verbonden? De analogie tussen ruimte en water is treffend: net zoals je in water kunt zwemmen, kun je door de ruimte heenlopen, of zweven, zonder plekken tegen te komen waar “geen ruimte” is.
Recentelijk zijn er in de natuurkunde aanwijzingen gevonden dat de verbondenheid van ruimte, net als de verbondenheid van water, emergent is. Dat wil zeggen dat op een fundamenteel niveau – grofweg op de Planckschaal, oftewel 10-35 meter – ruimte niet verbonden is. En een ruimte die niet verbonden is, kun je haast geen ruimte noemen.
Maar als er op kleine schaal geen ruimte is, wat is dan de oorsprong van ruimte? Net zoals water uit H2O-moleculen bestaat, verwachten we dat ruimte ook uit kleinere bouwstenen is opgebouwd.
Verstrengelingsentropie
Er bestaat inderdaad een voorstel voor deze bouwstenen van de ruimte. Om dit voorstel te begrijpen moet ik eerst een ander begrip introduceren: verstrengeling. Verstrengeling is een belangrijk fenomeen uit de quantummechanica, waarbij twee of meer deeltjes zodanig zijn verbonden, dat het ene deeltje niet meer volledig beschreven kan worden zonder het andere deeltje te noemen. Twee deeltjes kunnen zo sterk met elkaar verstrengeld zijn dat een meting aan het ene deeltje invloed heeft op de toestand van het andere deeltje. Verstrengeling wordt vaak beschreven aan de hand van een grootheid die we de verstrengelingsentropie, aangeduid met S, noemen.
De Canadese natuurkundige Mark van Raamsdonk was een van de eersten die de verbondenheid van ruimte aan het begrip verstrengeling koppelde. Zijn hypothese is dat de verbondenheid van ruimte voortkomt uit de verstrengeling van microscopische toestanden. Je kunt je de verstrengeling als een soort lijm voorstellen die alle microtoestanden bij elkaar houdt. De lijm (vergelijkbaar met de waterstofbruggen tussen H2O-moleculen) zorgt er uiteindelijk voor dat ruimte op macroniveau verbonden is.
Van Raamsdonks hypothese is een zeer kwalitatieve uitspraak, maar we kunnen haar ook kwantitatief maken. Van Raamsdonk baseerde zijn hypothese oorspronkelijk op een eenvoudige formule, die van toepassing is op de volgende situatie. Stel je voor dat we de ruimte in twee gebieden opdelen A en B (we nemen voor het gemak een vierkant) zoals weergegeven in het linkerdeel van afbeelding 2. Dan geldt de volgende formule
S = A/4G
waarbij de verstrengelingsentropie S een maat is voor de hoeveelheid verstrengeling tussen de twee gebieden A en B; A is de oppervlakte (“area”) die de twee gebieden scheidt; en G is de zwaartekrachtsconstante van Newton. Let op dat we het oppervlak in de figuur hieronder weergeven met een (stippel)lijn. Je moet dus eigenlijk een extra dimensie erbij denken, zodat het vierkant een doos wordt. A en B worden dan inderdaad gescheiden door een oppervlak.
Samengevat, hebben we dus gezien dat er een formule bestaat die een maat voor verstrengeling (de verstrengelingsentropie) gelijkstelt aan een meetkundige grootheid (de oppervlakte).
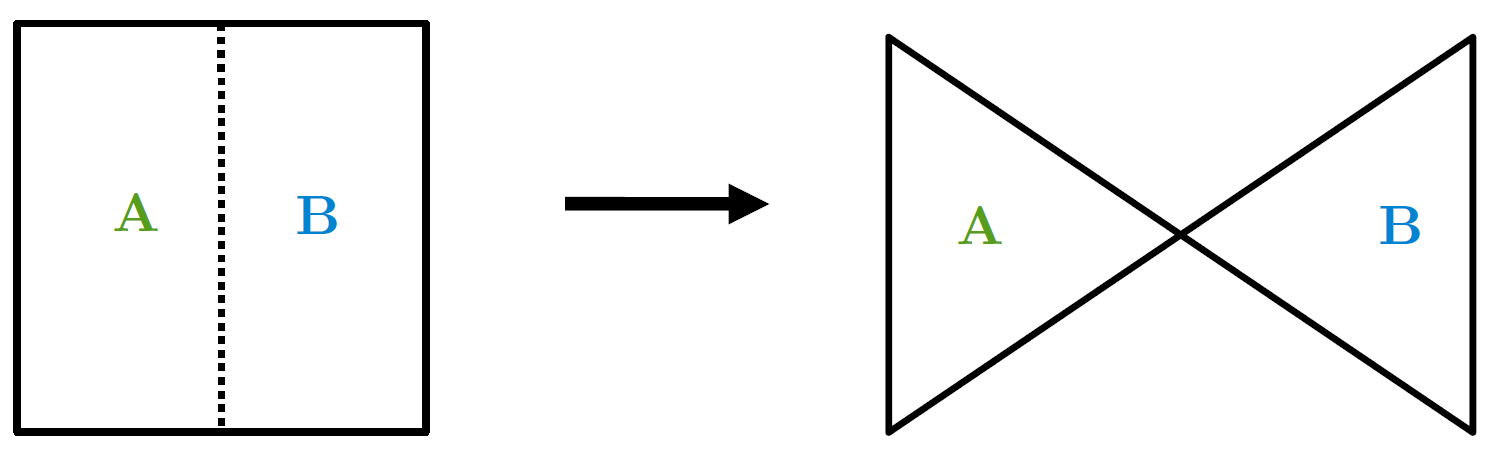
Afbeelding 2. Gedachte-experiment.
Stel dat we de ruimte in twee gebieden, A en B, opdelen (zie linkerfiguur). Dan is de oppervlakte van het scheidingsvlak – hier weergegeven door een stippellijn – een maat voor de verstrengeling tussen A en B. Als we de verstrengeling nu steeds kleiner maken, dan verwijderen de gebieden A en B zich van elkaar (zie rechterfiguur). Hieruit kunnen we concluderen dat de verbondenheid van ruimte voortkomt uit verstrengeling op quantumniveau.
Een gedachte-experiment
Laten we nu het volgende gedachte-experiment uitvoeren. Stel dat we de verstrengelingsentropie steeds kleiner maken, dan zegt bovenstaande formule dat de oppervlakte tussen twee gebieden A en B ook kleiner wordt. Zoals je in afbeelding 2 kunt zien, resulteert dit erin dat de gebieden A en B van elkaar gescheiden worden. En als we zover gaan dat er geen verstrengeling meer is tussen de gebieden, dan worden A en B slechts gescheiden door een punt, aangezien het oppervlak dat A en B scheidt er niet meer is (zie rechterfiguur). Met andere woorden: als er geen verstrengeling is tussen de ruimtes A en B, dan zijn ze niet met elkaar verbonden. We kunnen dit ook omdraaien: als A en B wel verstrengeld zijn (en de verstrengelingsentropie S niet nul is), dan resulteert dat in de verbondenheid van de gebieden A en B. We concluderen dus dat de formule ons vertelt dat de verbondenheid van ruimte voortkomt uit verstrengeling! Dit komt overeen met Van Raamsdonks hypothese.
We zijn dus aan de hand van een simpel gedachte-experiment tot de conclusie gekomen dat ruimte wellicht “bij elkaar wordt gehouden” door verstrengeling op quantumniveau. We benadrukken echter dat dit slechts een vermoeden is. Echt onomstotelijk bewijs voor dit idee bestaat (nog) niet. Maar dit gedachte-experiment leert ons in ieder geval erg veel over de oorsprong van ruimte en zwaartekracht. In het huidige onderzoek staan ideeën over verstrengeling, entropie en ruimte volop in de belangstelling. Zij worden op dit moment gebruikt om fundamentele vragen over quantumzwaartekracht te beantwoorden.
Referentie: M. Van Raamsdonk, Comments on quantum gravity and entanglement, (2009), http://arxiv.org/pdf/0907.2939v2.pdf
De afbeelding in het blokkenschema is afkomstig uit de film The Matrix.