Afbeelding 1. Een orkest.Door goed naar de “tonen” van de natuur te luisteren kunnen we van alles leren over zwarte gaten, het binnenste van de aarde of het quark-gluonplasma! Foto: Vienna Mozart Orchestra.
In het artikel Waarom klinkt een gitaar anders dan een piano? hebben we de trillingen van een snaar ontleed. Elke trilling blijkt opgebouwd te zijn uit een hele rits tonen, of eigentrillingen. In het artikel Hoor je de vorm van een trommel? beargumenteerden we verder dat trillingen op trommelvellen en zelfs vibraties van de ruimtetijd, de zogenaamde zwaartekrachtsgolven, voldoen aan dezelfde wiskundige trillingswetten die gelden voor een snaar. In dit artikel nemen we ook dempingen van de trillingen mee. De specifieke tijd waarmee een trilling uitdooft verschaft meer informatie dan (en: als) je denkt.
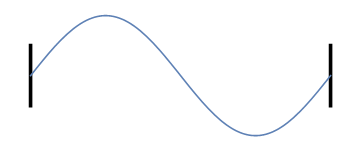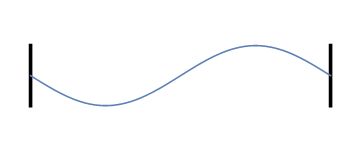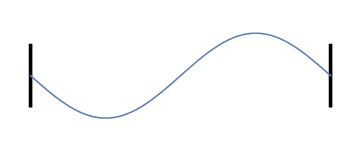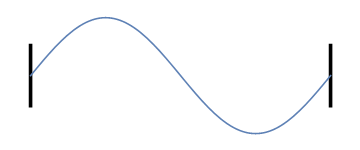
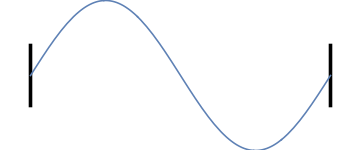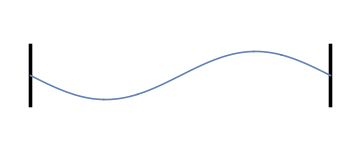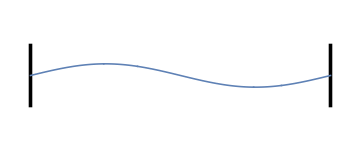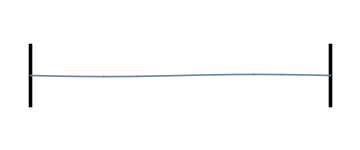
Laten we weer nadenken over trillingen op een koord of snaar, maar ditmaal met demping. Herinner je uit de vorige artikelen dat, wanneer we het koord of de snaar aan de uiteinden vastmaken en laten trillen op een bepaalde frequentie, het resultaat als volgt was (klik op het plaatje om de bijbehorende toon te horen):
Maar wat gebeurt er als we nu bijvoorbeeld luchtwrijving meenemen, of als we die uiteinden van schokabsorberend rubber laten zijn? Dan zal er trillingsenergie wegvloeien. Het wegvloeien van energie uit een systeem heet met een duur woord dissipatie. Hier zie je wat er gebeurt als we het ingrediënt dissipatie toevoegen aan het trillende koord:
De trillingen zonder dissipatie, zoals in het eerste plaatje, komen in de natuur eigenlijk helemaal niet voor. Als je op de verschillende plaatjes klikt hoor je een trilling van exact 440 Hertz (440 trillingen per seconde) en je hoort meteen dat het geluid met dissipatie veel natuurlijker klinkt dan het ideale geval (al zal je er nog steeds geen volle zalen mee trekken).
Zoals eerder uitgelegd bestaan alle trillingen uit verschillende tonen. De dissipatieloze tonen die we tot nu toe beschouwd hebben, zijn de zogenaamde normale tonen. De tonen mét dissipatie heten ook wel quasinormale tonen; bijna-normale tonen dus. Bij quasinormale tonen hoort een specifieke levensduur. Deze specifieke levensduur geeft aan hoelang nadat je een specifieke quasinormale toon hebt aangeslagen, je die toon nog kunt horen. (Iets preciezer: de levensduur is gedefinieerd als de tijd tot de demping een factor 1/e, oftewel zo’n 37% is.) Deze specifieke levensduur heet ook wel de relaxatietijd. Zie onderstaande afbeelding:
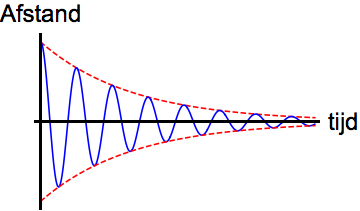
Afbeelding 2. Een gedempte trilling.De tijd waarin de trilling is dempt tot zo’n 37% van zijn oorspronkelijke uitwijking heet de relaxatietijd.
De quasinormale tonen en hun relaxatietijd zijn een essentieel ingrediënt voor het kunnen “luisteren” en herkennen van geluiden (die opgebouwd zijn uit vele quasinormale tonen).
Wat heeft dit met zwarte gaten te maken? Je kunt een zwart gat (wiskundig gezien) een beetje platdrukken. Als je het zwarte gat dan loslaat, zal het zich na verloop van tijd herstellen tot een volledig rond zwart gat. Bij dit proces ontstaan quasinormale “tonen” als trillingen in de ruimtetijd: zwaartekrachtsgolven. Hieronder zie je de verschillende trillingspartonen en relaxatietijden voor de theoretisch voorspelde zwaartekrachtsgolven voor diversee astrofysische processen:
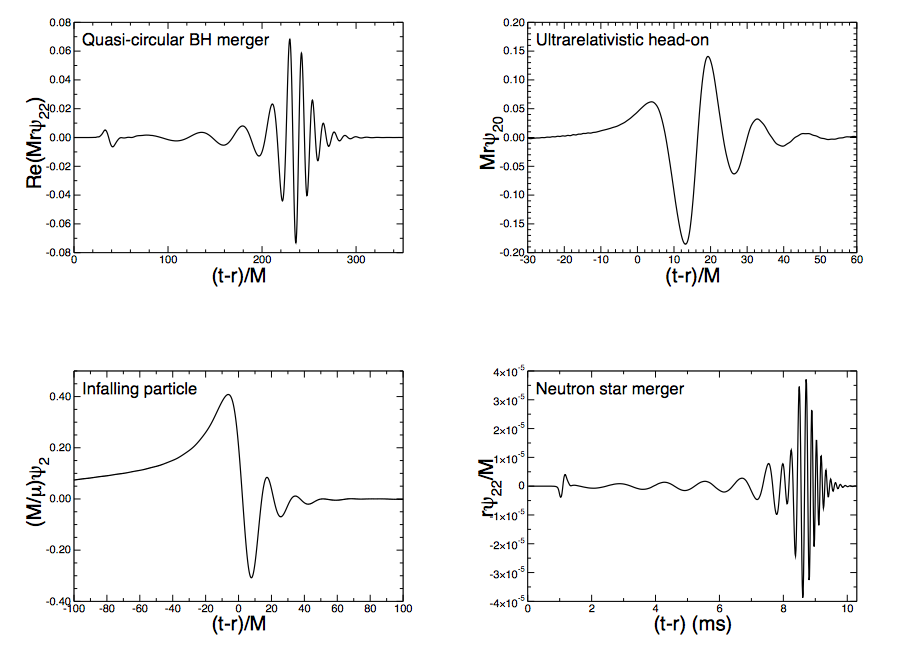
Afbeelding 3. Zwaartekrachtsgolven van diverse astrofysische processen.In al deze processen zijn gedempte trillingen te zien. Afbeelding uit Quasinormal modes of black holes and black branes van E. Berti, V. Cardoso en A. O. Starinets.
Wanneer de metingen aan gravitatiegolven nauwkeuriger worden, kunnen we aan de hand van deze patronen verschillende fysische processen gaan herkennen: nabije toekomstmuziek dus!
Laten we nog een voorbeeld noemen waarin quasinormale tonen handig zijn. Aardbevingen zijn vreselijk, laten we dat voorop stellen. Maar als ze dan toch plaatsvinden, kunnen we ze net zo goed meten. Voor aardbevingen die krachtig genoeg zijn, kun je de quasinormale tonen van de aarde meten! Deze quasinormale tonen geven ons informatie over het binnenste van de aarde, een mysterieuze plek waar we vrij weinig over weten. Verschillende typen materie, op verschillende diepten, trillen op verschillende wijze mee en op die manier kun je informatie ontfutselen aan het binnenste van onze aarde.
Tot slot is nog zo’n mysterieus systeem het quark-gluonplasma, een soort van gloeiend hete deeltjesoersoep die bij botsingen van deeltjes in deeltjesversnellers en in het vroege heelal tijdelijk ontstaat. Onze gebruikelijke modellen weten niet echt raad met dit plasma. Via de holografie kan men voor een systeem dat heel erg lijkt op het quark-gluonplasma een belangrijke fysische eigenschap, de schuifviscositeit, berekenen. De holografie wordt hier gebruikt door het systeem dat lijkt op het quark-gluonplasma te “vertalen” naar een bepaald zwart gat. Het hele eiereneten van holografie is dat, hoewel deze systemen er onderling heel anders uitzien, ze toch wiskundig hetzelfde zijn – mits je natuurlijk weet hoe je de vertaalslag tussen de twee systemen moet maken.
De vraag na hoelang een drukverstoring is uitgewerkt in het plasma is zeer lastig. Via holografie kunnen we dit varkentje echter relatief eenvoudig wassen. Het blijkt zo te zijn dat de relaxatietijden van de quasinormale tonen die horen bij het weer rond worden van het platgedrukte zwarte gat, de tijd voorspellen waarin de drukverstoring in het quark-gluonplasma is uitgewerkt!
De moraal van het verhaal is dat we nu natuurkundig aannemelijk hebben gemaakt wat je oma waarschijnlijk ook al zei: dat je altijd goed moet luisteren!